Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T21:59:33.420Z Has data issue: false hasContentIssue false
  • English
  • Français

WHEN LATTICE HOMOMORPHISMS OF ARCHIMEDEAN VECTOR LATTICES ARE RIESZ HOMOMORPHISMS

Part of: Topological linear spaces and related structures

Published online by Cambridge University Press:  09 October 2009

MOHAMED ALI TOUMI
MOHAMED ALI TOUMI*
Affiliation:
Département de Mathématiques, Faculté des Sciences de Bizerte, 7021, Zarzouna, Bizerte, Tunisia (email: mohamedali.toumi@fsb.rnu.tn)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A, B be Archimedean vector lattices and let (ui)i∈I, (vi)i∈I be maximal orthogonal systems of A and B, respectively. In this paper, we prove that if T is a lattice homomorphism from A into B such that 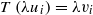for each λ∈ℝ+ and i∈I, then T is linear. This generalizes earlier results of Ercan and Wickstead (Math. Nachr279 (9–10) (2006), 1024–1027), Lochan and Strauss (J. London Math. Soc. (2) 25 (1982), 379–384), Mena and Roth (Proc. Amer. Math. Soc.71 (1978), 11–12) and Thanh (Ann. Univ. Sci. Budapest. Eotvos Sect. Math.34 (1992), 167–171).

Keywords

weak order unitlattice homomorphismRiesz homomorphism

MSC classification

Secondary: 46A40: Ordered topological linear spaces, vector lattices
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 87 , Issue 2 , October 2009 , pp. 263 - 273
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2009

References

[1]Aliprantis, C. D. and Burkinshaw, O., Positive Operators (Academic Press, Orlando, FL, 1985).Google Scholar
[2]De Pagter, B., f-Algebras and orthomorphisms. Thesis, Leiden, 1981.Google Scholar
[3]Ercan, Z. and Wickstead, A. W., ‘When a lattice homomorphism is a Riesz homomorphism’, Math. Nachr. 279(9–10) (2006), 1024–1027.CrossRefGoogle Scholar
[4]Lochan, R. and Strauss, D., ‘Lattice homomorphisms of spaces of continuous functions’, J. London Math. Soc. (2) 25 (1982), 379–384.CrossRefGoogle Scholar
[5]Luxemburg, W. A. J. and Zaanen, A. C., Riesz Spaces I (North-Holland, Amsterdam, 1971).Google Scholar
[6]Mena, R. and Roth, B., ‘Homomorphisms of lattices on continuous functions’, Proc. Amer. Math. Soc. 71 (1978), 11–12.CrossRefGoogle Scholar
[7]Schaefer, H. H., Banach Lattices and Positive Operators, Grundlehren Math. Wiss., 215 (Springer, Berlin, 1974).CrossRefGoogle Scholar
[8]Thanh, D. T., ‘A generalization of a theorem of R. Mena and B. Roth’, Ann. Univ. Sci. Budapest. Eotvos Sect. Math. 34 (1992), 167–171.Google Scholar