Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T04:43:13.872Z Has data issue: false hasContentIssue false
  • English
  • Français

CATEGORICAL PROOF OF HOLOMORPHIC ATIYAH–BOTT FORMULA

Part of: Algebraic geometry: Foundations General theory of categories and functors Homological algebra

Published online by Cambridge University Press:  20 December 2018

Grigory Kondyrev  and
Artem Prikhodko
Grigory Kondyrev
Affiliation:
National Research University Higher School of Economics, Russian Federation (gkondyrev@gmail.com)
Artem Prikhodko
Affiliation:
National Research University Higher School of Economics, Russian Federation, Center for Advanced Studies, Skoltech, Moscow, Russian Federation (artem.n.prihodko@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a $2$-commutative diagram

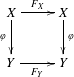
in a symmetric monoidal 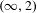$(\infty ,2)$-category 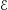$\mathscr{E}$ where 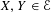$X,Y\in \mathscr{E}$ are dualizable objects and $\unicode[STIX]{x1D711}$ admits a right adjoint we construct a natural morphism $\mathsf{Tr}_{\mathscr{E}}(F_{X})\xrightarrow[{}]{~~~~~}\mathsf{Tr}_{\mathscr{E}}(F_{Y})$ between the traces of 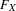$F_{X}$ and 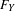$F_{Y}$, respectively. We then apply this formalism to the case when 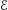$\mathscr{E}$ is the 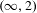$(\infty ,2)$-category of $k$-linear presentable categories which in combination of various calculations in the setting of derived algebraic geometry gives a categorical proof of the classical Atiyah–Bott formula (also known as the Holomorphic Lefschetz fixed point formula).

Keywords

tracesfixed-points formulas2-categories

MSC classification

Primary: 14A99: None of the above, but in this section 18A99: None of the above, but in this section
Secondary: 18G99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1739 - 1763
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atiyah, M. F. and Bott, R, A Lefschetz fixed point formula for elliptic complexes I, Ann. of Math. (2) 86(2) (1967), 374–407.Google Scholar
Atiyah, M. F. and Bott, R., A Lefschetz fixed point formula for elliptic complexes II. Applications, Ann. of Math. (2) 88(3) (1968), 451–491.Google Scholar
Ben-Zvi, D., Francis, J. and Nadler, D., Integral transforms and Drinfeld centers in derived algebraic geometry, J. Amer. Math. Soc. 23(4) (2010), 909–966.Google Scholar
Ben-Zvi, D. and Nadler, D., Nonlinear traces, Preprint, 2013, available at arXiv:1305.7175v3.Google Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry, available at http://www.math.harvard.edu/∼gaitsgde/GL/.Google Scholar
Lefschetz, S., Intersections and transformations of complexes and manifolds, Trans. Amer. Math. Soc. 28 (1926), 1–49.Google Scholar
Lurie, J., Higher algebra, available at http://www.math.harvard.edu/∼lurie/papers/HA.pdf.Google Scholar