Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T15:13:42.222Z Has data issue: false hasContentIssue false
  • English
  • Français

ISOTROPIC MOTIVES

Part of: $K$-theory in geometry Cycles and subschemes (Co)homology theory

Published online by Cambridge University Press:  22 December 2020

Alexander Vishik Open the ORCID record for Alexander Vishik [Opens in a new window]
Alexander Vishik*
Affiliation:
School of Mathematical Sciences, University of Nottingham, University Park, Nottingham, NG7 2RD, UK (alexander.vishik@nottingham.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we introduce the local versions of the Voevodsky category of motives with 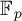$\mathbb{F} _p$ -coefficients over a field k, parametrized by finitely generated extensions of k. We introduce the so-called flexible fields, passage to which is conservative on motives. We demonstrate that, over flexible fields, the constructed local motivic categories are much simpler than the global one and more reminiscent of a topological counterpart. This provides handy ‘local’ invariants from which one can read motivic information. We compute the local motivic cohomology of a point for 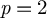$p=2$ and study the local Chow motivic category. We introduce local Chow groups and conjecture that over flexible fields these should coincide with Chow groups modulo numerical equivalence with $\mathbb{F} _p$ -coefficients, which implies that local Chow motives coincide with numerical Chow motives. We prove this conjecture in various cases.

Keywords

motivemotivic cohomologyChow groupsnumerical equivalence of cyclesMilnor's operations

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives
Secondary: 14C25: Algebraic cycles 19E15: Algebraic cycles and motivic cohomology 14F42: Motivic cohomology; motivic homotopy theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 4 , July 2022 , pp. 1271 - 1330
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bachmann, T., On the invertibility of motives of affine quadrics, Doc. Math. 22 (2017), 363–395.Google Scholar
Brosnan, P., Steenrod operations in Chow theory, Trans. Amer. Math. Soc. 355(5) (2003), 1869–1903.CrossRefGoogle Scholar
Cisinski, D.-C. and Déglise, F., Local and stable homological algebra in Grothendieck abelian categories, Homology, Homotopy Appl. 11(1) (2009), 219–260.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Levine, M., Une version du théorème d’Amer et Brumer pour les zéro-cycles [A version of the theorem of Amer and Brumer on zero-cycles (in French)]. arxiv.org/abs/0911.4644.Google Scholar
Fulton, W., Intersection Theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3)2 [Modern Surveys in Mathematics (3) 2] (Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1984).CrossRefGoogle Scholar
Gille, S. and Vishik, A., Rost nilpotence and free theories, Documenta Math. 23 (2018), 1635–1657.Google Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. I,II, Ann. Math.(2) 79 (1964), 109–203; ibid.79 (1964), 205–326.CrossRefGoogle Scholar
Hoffmann, D. and Izhboldin, O., Embeddability of quadratic forms in Pfister forms, Indag. Mathem., N.S. (2) 11 (2000), 219–237.CrossRefGoogle Scholar
Levine, M. and Morel, F., Algebraic Cobordism , Springer Monographs in Mathematics (Springer-Verlag, Berlin, Heidelberg, New York, 2007).Google Scholar
Orlov, D., Vishik, A. and Voevodsky, V., An exact sequence for ${K}_{\ast}^M/2$ with applications to quadratic forms, Ann. Math. 165(1) (2007), 1–13.CrossRefGoogle Scholar
Panin, I. and Smirnov, A., ‘Push-forwards in oriented cohomology theories of algebraic varieties’, K-theory preprint archive, 459, 2000, http://www.math.uiuc.edu/K-theory/0459/.Google Scholar
Rost, M., ‘The motive of a Pfister form’, Preprint, 1998, www.math.uni-bielefeld.de/~rost/data/motive.pdf.Google Scholar
Soule, C. and Voisin, C., Torsion cohomology classes and algebraic cycles on complex projective manifolds, Adv. Math. 198(1) (2005), 107–127.CrossRefGoogle Scholar
Vishik, A., ‘Integral motives of quadrics’, MPIM Preprint, 1998 (13), 1-82, www.mpim-bonn.mpg.de/node/263.Google Scholar
Vishik, A., ‘On the kernels in Milnor’s K-theory under function field extensions’, MPIM Preprint, March 30, 1998, www.mpim-bonn.mpg.de/node/263.Google Scholar
Vishik, A., Symmetric operations in algebraic cobordism, Adv. Math. 213 (2007), 489–552.CrossRefGoogle Scholar
Vishik, A., Affine quadrics and the Picard group of the motivic category, Compositio Math. 155 (2019), 1500–1520.CrossRefGoogle Scholar
Vishik, A., Stable and unstable operations in algebraic cobordism, Ann. Scient. l’Ecole Norm. Sup. (4) 52 (2019), 561–630.CrossRefGoogle Scholar
Voevodsky, V., ‘Bloch-Kato conjecture for $\mathbb{Z}/2$ -coefficients and algebraic Morava K-theories’, Preprint, 1995, www.math.uiuc.edu/K-theory/0076.Google Scholar
Voevodsky, V., Triangulated categories of motives over a field, in Cycles, Transfers and Motivic Homology Theories (Princeton University Press, Princeton, NJ, 2000), 188–238.Google Scholar
Voevodsky, V., Reduced power operations in motivic cohomology, Publ. Math. IHES 98 (2003), 1–57.CrossRefGoogle Scholar
Voevodsky, V., Motivic cohomology with $\mathbb{Z}/ 2$ -coefficients, Publ. Math. IHES 98 (2003), 59–104.CrossRefGoogle Scholar
Yagita, N., Applications of Atiah-Hirzebruch spectral sequences for motivic cobordisms, Proc. London Math. Soc. 90 (2005), 783–816.CrossRefGoogle Scholar