Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T00:13:59.818Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC ISOMONODROMIC DEFORMATIONS AND THE MAPPING CLASS GROUP

Part of: Differential equations in the complex domain (Co)homology theory Families, fibrations Special aspects of infinite or finite groups

Published online by Cambridge University Press:  18 November 2019

Gaël Cousin Open the ORCID record for Gaël Cousin [Opens in a new window]  and
Viktoria Heu
Gaël Cousin
Affiliation:
GMA-IME, Universidade Federal Fluminense, Campus do Gragoatá, Niterói, RJ, Brazil (gcousin@id.uff.br)
Viktoria Heu
Affiliation:
IRMA, 7 rue René Descartes, 67084Strasbourg, France (heu@math.unistra.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

The germ of the universal isomonodromic deformation of a logarithmic connection on a stable $n$-pointed genus $g$ curve always exists in the analytic category. The first part of this article investigates under which conditions it is the analytic germification of an algebraic isomonodromic deformation. Up to some minor technical conditions, this turns out to be the case if and only if the monodromy of the connection has finite orbit under the action of the mapping class group. The second part of this work studies the dynamics of this action in the particular case of reducible rank 2 representations and genus 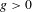$g>0$, allowing to classify all finite orbits. Both of these results extend recent ones concerning the genus 0 case.

Keywords

isomonodromic deformationsmapping class group

MSC classification

Primary: 20F36: Braid groups; Artin groups 34M56: Isomonodromic deformations
Secondary: 14D05: Structure of families (Picard-Lefschetz, monodromy, etc.) 14F35: Homotopy theory; fundamental groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 5 , September 2021 , pp. 1497 - 1545
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors would like to warmly thank Gwenaël Massuyeau for discussions around the mapping class group. We are also grateful to the anonymous referee for useful suggestions. This work took place at IRMA and LAREMA. It was supported by ANR-13-BS01-0001-01, ANR-13-JS01-0002-01 and Labex IRMIA.

References

Arbarello, E., Cornalba, M. and Griffiths, P. A., Geometry of Algebraic Curves. Vol. II, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 268 (Springer, Heidelberg, 2011). With a contribution by Joseph Daniel Harris.Google Scholar
Artin, E., Theorie der Zöpfe, Abh. Math. Semin. Univ. Hambg. 4(1) (1925), 47–72.Google Scholar
Baily, W. L. Jr., On the automorphism group of a generic curve of genus ${>}2$ , J. Math. Kyoto Univ., 1 (1961/1962), 101–108; correction, 325.}2$+,+J.+Math.+Kyoto+Univ.,+1+(1961/1962),+101–108;+correction,+325.>Google Scholar
Biswas, I., Gupta, S., Mj, M. and Whang, J. P., Surface group representations in $\text{SL}_{2}(\mathbb{C})$ with finite mapping class orbits, preprint, 2017, arXiv:1707.00071, version 3, issued in 2019.Google Scholar
Cornalba, M., Erratum: ‘On the locus of curves with automorphisms’ [Ann. Mat. Pura Appl. (4) 149 (1987), 135–151; mr0932781], Ann. Mat. Pura Appl. (4) 187(1) (2008), 185–186.Google Scholar
Cousin, G., Projective representations of fundamental groups of quasiprojective varieties: a realization and a lifting result, C. R. Math. Acad. Sci. Paris 353(2) (2015), 155–159.Google Scholar
Cousin, G., Algebraic isomonodromic deformations of logarithmic connections on the Riemann sphere and finite braid group orbits on character varieties, Math. Ann. 367(3–4) (2017), 965–1005.Google Scholar
Cousin, G. and Moussard, D., Finite braid group orbits in Aff(C)-character varieties of the punctured sphere, Int. Math. Res. Not. IMRN 2018(11) (2018), 3388–3442.Google Scholar
Debarre, O., Higher-dimensional Algebraic Geometry, Universitext (Springer, New York, 2001).Google Scholar
Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, Volume 163 (Springer, Berlin, 1970).Google Scholar
Farb, B. and Margalit, D., A Primer on Mapping Class Groups, Princeton Mathematical Series, Volume 49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Heu, V., Universal isomonodromic deformations of meromorphic rank 2 connections on curves, Ann. Inst. Fourier (Grenoble) 60(2) (2010), 515–549.Google Scholar
Hubbard, J. H., Teichmüller Theory and Applications to Geometry, Topology, and Dynamics. Vol. 1. Matrix Editions, Ithaca, NY, 2006. Teichmüller theory, With contributions by Adrien Douady, William Dunbar, Roland Roeder, Sylvain Bonnot, David Brown, Allen Hatcher, Chris Hruska and Sudeb Mitra, With forewords by William Thurston and Clifford Earle.Google Scholar
Husemoller, D., Fibre Bundles, 3rd edn, Graduate Texts in Mathematics, Volume 20 (Springer, New York, 1994).Google Scholar
Krichever, I., Isomonodromy equations on algebraic curves, canonical transformations and Whitham equations, Mosc. Math. J. 2(4) (2002), 717–752, 806.Google Scholar
Lickorish, W. B. R., A finite set of generators for the homeotopy group of a 2-manifold, Proc. Cambridge Philos. Soc. 60 (1964), 769–778.Google Scholar
Malgrange, B., Sur les déformations isomonodromiques. I et II, in Progress in Mathematics, Volume 37, pp. 401–438 (Birkhäuser Boston, Boston, MA, 1983).Google Scholar
Monsky, P., The automorphism groups of algebraic curves, PhD thesis, The University of Chicago, ProQuest LLC, Ann Arbor, MI (1962).Google Scholar
Poonen, B., Varieties without extra automorphisms. I. Curves, Math. Res. Lett. 7(1) (2000), 67–76.Google Scholar
Serre, J.-P., Géométrie algébrique et géométrie analytique, Ann. Inst. Fourier (Grenoble) 6 (1955–1956), 1–42.Google Scholar