Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T09:32:03.974Z Has data issue: false hasContentIssue false
  • English
  • Français

EQUIVALENT NORMS WITH AN EXTREMELY NONLINEABLE SET OF NORM ATTAINING FUNCTIONALS

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  13 February 2018

Vladimir Kadets ,
Ginés López ,
Miguel Martín  and
Dirk Werner
Vladimir Kadets
Affiliation:
School of Mathematics and Informatics, V. N. Karazin Kharkiv National University, pl. Svobody 4, 61022 Kharkiv, Ukraine (vova1kadets@yahoo.com)
Ginés López
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain (glopezp@ugr.es; mmartins@ugr.es)
Miguel Martín
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain (glopezp@ugr.es; mmartins@ugr.es)
Dirk Werner
Affiliation:
Department of Mathematics, Freie Universität Berlin, Arnimallee 6, D-14195 Berlin, Germany (werner@math.fu-berlin.de)
Get access
Rights & Permissions [Opens in a new window]

Abstract

We present a construction that enables one to find Banach spaces 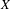$X$ whose sets 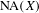$\operatorname{NA}(X)$ of norm attaining functionals do not contain two-dimensional subspaces and such that, consequently, 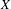$X$ does not contain proximinal subspaces of finite codimension greater than one, extending the results recently provided by Read [Banach spaces with no proximinal subspaces of codimension 2, Israel J. Math. (to appear)] and Rmoutil [Norm-attaining functionals need not contain 2-dimensional subspaces, J. Funct. Anal. 272 (2017), 918–928]. Roughly speaking, we construct an equivalent renorming with the requested properties for every Banach space 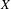$X$ where the set 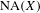$\operatorname{NA}(X)$ for the original norm is not “too large”. The construction can be applied to every Banach space containing 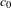$c_{0}$ and having a countable system of norming functionals, in particular, to separable Banach spaces containing 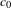$c_{0}$. We also provide some geometric properties of the norms we have constructed.

Keywords

norm attaining functionalsrenormings of Banach spacesnonlineable setsproximinal subspaces

MSC classification

Primary: 46B03: Isomorphic theory (including renorming) of Banach spaces 46B04: Isometric theory of Banach spaces
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 1 , January 2020 , pp. 259 - 279
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acosta, M. D., Denseness of norm-attaining operators into strictly convex spaces, Proc. Roy. Soc. Edinburgh 129A (1999), 1107–1114.Google Scholar
Acosta, M. D., Norm-attaining operators into L 1(𝜇), in Function Spaces. Proceedings of the 3rd Conference, Edwardsville, IL, USA, May 19–23, 1998 (ed. Jarosz, K.), Contemporary Mathematics, Volume 232, pp. 1–11 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Acosta, M. D., Aizpuru, A., Aron, R. M. and García-Pacheco, F., Functionals that do not attain their norm, Bull. Belg. Math. Soc. Simon Stevin 14 (2007), 407–418.Google Scholar
Albiac, F. and Kalton, N., Topics in Banach Space Theory, second edition, Graduate Texts in Mathematics, Volume 233 (Springer, New York, 2016).Google Scholar
Banach, S., Théorie des Opérations Linéaires, Monografie Matematyczne, Volume 1 (Seminarium Matematyczne Uniwersytetu Warszawskiego, Instytut Matematyczny PAN, Warszawa, 1932).Google Scholar
Bandyopadhyay, P. and Godefroy, G., Linear structures in the set of norm-attaining functionals on a Banach space, J. Convex Anal. 13 (2006), 489–497.Google Scholar
Bogachev, V. I., Measure Theory, Volume II (Springer, New York, 2007).Google Scholar
Bourgain, J., On dentability and the Bishop-Phelps property, Israel J. Math. 28 (1977), 265–271.Google Scholar
Bourgain, J., La propriété de Radon-Nikodým, Publ. Math. Univ. Pierre Marie Curie 36 (1979).Google Scholar
Bourgin, R. R., Geometric Aspects of Convex Sets with the Radon-Nikodym Property, Lecture Notes in Mathematics, Volume 993 (Springer, Berlin–Heidelberg–New York, 1983).Google Scholar
Cross, R. W., On the continuous linear image of a Banach space, J. Aust. Math. Soc. (Series A) 29 (1980), 219–234.Google Scholar
Cross, R. W., Ostrovskii, M. I. and Shevchik, V. V., Operator ranges in Banach spaces I, Math. Nachr. 173 (1995), 91–114.Google Scholar
Dancer, E. N. and Sims, B., Weak star separability, Bull. Aust. Math. Soc. 20 (1979), 253–257.Google Scholar
Debs, G., Godefroy, G. and Saint Raymond, J., Topological properties of the set of norm-attaining linear functionals, Canad. J. Math. 47 (1995), 318–329.Google Scholar
Deville, R., Godefroy, G. and Zizler, V., Smoothness and Renormings in Banach Spaces, Pitman Monographs and Surveys in Pure and Applied Mathematics, Volume 64 (Longman Scientific & Technical, London, 1993).Google Scholar
Diestel, J., Geometry of Banach Spaces. Selected Topics, Lecture Notes in Mathematics, Volume 485 (Springer, Berlin–Heidelberg–New York, 1975).Google Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos, V., Pelant, J. and Zizler, V., Functional Analysis and Infinite-Dimensional Geometry (Springer, New York, 2001).Google Scholar
Fillmore, P. A. and Williams, J. P., On operator ranges, Adv. Math. 7 (1971), 254–281.Google Scholar
Fonf, V. and Lindenstrauss, J., Boundaries and generation of convex sets, Israel J. Math. 136 (2003), 157–172.Google Scholar
Godefroy, G., The Banach space c 0 , Extracta Math. 16 (2001), 1–25.Google Scholar
Harmand, P., Werner, D. and Werner, W., M-Ideals in Banach Spaces and Banach Algebras, Lecture Notes in Mathematics, Volume 1547 (Springer, Berlin–Heidelberg–New York, 1993).Google Scholar
Kadets, V. M., López, G. and Martín, M., Some geometric properties of Read’s space, J. Funct. Anal. 274(3) (2018), 889–899.Google Scholar
Kaufman, R., Topics on analytic sets, Fund. Math. 139 (1991), 215–229.Google Scholar
Kelley, J. L. and Namioka, I., Linear Topological Spaces, Graduate Texts in Mathematics, Volume 36 (Springer, New York, 1976).Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces I: Sequence Spaces (Springer, New York, 1977).Google Scholar
Nygaard, O., Thick sets in Banach spaces and their properties, Quaest. Math. 29 (2006), 59–72.Google Scholar
Partington, J. R., Equivalent norms on spaces of bounded functions, Israel J. Math. 35 (1980), 205–209.Google Scholar
Read, C. J., Banach spaces with no proximinal subspaces of codimension 2, Israel J. Math. doi:10.1007/s11856-017-1627-3.Google Scholar
Rmoutil, M., Norm-attaining functionals need not contain 2-dimensional subspaces, J. Funct. Anal. 272 (2017), 918–928.Google Scholar
Rogers, C. A. and Jayne, J., K-analytic sets, in Analytic Sets (ed. Rogers, C. A. et al. ), pp. 1–181 (Academic Press, London–New York–Toronto–Sydney–San Francisco, 1980).Google Scholar
Shevchik, V. V., On subspaces of a Banach space that coincide with the ranges of continuous linear operators, Rev. Roumaine Math. Pures Appl. 31 (1986), 65–71.Google Scholar
Singer, I., The theory of best approximation and functional analysis, in Conference Board of the Mathematical Sciences Regional Conference Series in Applied Mathematics, Volume 13 (Society for Industrial and Applied Mathematics, Philadelphia, PA, 1974).Google Scholar
Wilansky, A., Modern Methods in Topological Vector Spaces (McGraw-Hill, New York, 1978).Google Scholar