No CrossRef data available.
Article contents
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
Part of:
Algebraic groups
Lie groups
Singularities
Topological $K$-theory
Families, fibrations
Representation theory of groups
Published online by Cambridge University Press: 18 February 2015
Abstract
This paper deals with the geometric local theta correspondence at the Iwahori level for dual reductive pairs of type II over a non-Archimedean field 
$F$ of characteristic 
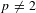$p\neq 2$ in the framework of the geometric Langlands program. First we construct and study the geometric version of the invariants of the Weil representation of the Iwahori-Hecke algebras. In the particular case of 
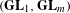$(\mathbf{GL}_{1},\mathbf{GL}_{m})$ we give a complete geometric description of the corresponding category. The second part of the paper deals with geometric local Langlands functoriality at the Iwahori level in a general setting. Given two reductive connected groups 
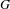$G$ and 
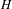$H$ over 
$F$, and a morphism 
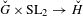${\check{G}}\times \text{SL}_{2}\rightarrow \check{H}$ of Langlands dual groups, we construct a bimodule over the affine extended Hecke algebras of 
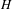$H$ and 
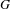$G$ that should realize the geometric local Arthur–Langlands functoriality at the Iwahori level. Then, we propose a conjecture describing the geometric local theta correspondence at the Iwahori level constructed in the first part in terms of this bimodule, and we prove our conjecture for pairs 
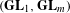$(\mathbf{GL}_{1},\mathbf{GL}_{m})$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 3 , July 2016 , pp. 625 - 671
- Copyright
- © Cambridge University Press 2015
References
Adams, J., L-functoriality for dual pairs, Astérisque 171–172 (1989), 85–129. Orbites unipotentes et représentations, II.Google Scholar
Arkhipov, S. and Bezrukavnikov, R., Perverse sheaves on affine flags and Langlands dual group, Israel J. Math. 170 (2009), 135–183. With an appendix by Bezrukavrikov and I. Mirković.CrossRefGoogle Scholar
Arthur, J., On some problems suggested by the trace formula, in Lie Group Representations, II (College Park, MD, 1982/1983), Lecture Notes in Mathematics, Volume 1041, pp. 1–49 (Springer, Berlin, 1984).Google Scholar
Aubert, A.-M., Correspondance de Howe et sous-groupes parahoriques, J. Reine Angew. Math. 392 (1988), 176–186.Google Scholar
Aubert, A.-M., Description de la correspondance de Howe en termes de classification de Kazhdan–Lusztig, Invent. Math. 103(2) (1991), 379–415.CrossRefGoogle Scholar
Beauville, A. and Laszlo, Y., Conformal blocks and generalized theta functions, Commun. Math. Phys. 164(2) (1994), 385–419.CrossRefGoogle Scholar
Beĭlinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers, in Analysis and Topology on Singular Spaces, I (Luminy, 1981), Astérisque, Volume 100, pp. 5–171 (Société Mathématique de France, Paris, 1982).Google Scholar
Beĭlinson, A. A. and Drinfeld, V., Quantization of Hitchin’s integrable systems and Hecke eigensheaves (1991).Google Scholar
Bernstein, J. N., Le ‘centre’ de Bernstein, in Representations of Reductive Groups Over a Local Field (ed. Deligne, P.), Travaux en Cours, pp. 1–32 (Hermann, Paris, 1984).Google Scholar
Bezrukavnikov, R., On two geometric realizations of an affine Hecke algebra, Preprint, 2012, arXiv:1209.0403.Google Scholar
Borel, A., Automorphic L-functions, in Automorphic Forms, Representations and L-Functions (Proc. Sympos. Pure Math., Oregon State University, Corvallis, OR, 1977), Part 2, Proceedings of Symposia in Pure Mathematics, Volume XXXIII, pp. 27–61.Google Scholar
Borel, A., Admissible representations of a semi-simple group over a local field with vectors fixed under an Iwahori subgroup, Invent. Math. 35 (1976), 233–259.Google Scholar
Bourbaki, N., Lie Groups and Lie Algebras. Chapters 4–6, Elements of Mathematics (Berlin) (Springer-Verlag, Berlin, 2002). Translated from the 1968 French original by Andrew Pressley.CrossRefGoogle Scholar
Chriss, N. and Ginzburg, V., Representation Theory and Complex Geometry (Birkhäuser Boston Inc., Boston, MA, 1997).Google Scholar
Farang-Hariri, B., La fonctorialité d’Arthur–Langlands locale géométrique et la correspondance de Howe au niveau Iwahori, C. R. Math. Acad. Sci. Paris 350(17–18) (2012), 813–816.Google Scholar
Frenkel, E. and Gaitsgory, D., Local geometric Langlands correspondence and affine Kac–Moody algebras, in Algebraic Geometry and Number Theory, Progress in Mathematics, Volume 253, pp. 69–260 (Birkhäuser, Boston, 2006).Google Scholar
Gaitsgory, D., Construction of central elements in the affine Hecke algebra via nearby cycles, Invent. Math. 144(2) (2001), 253–280.CrossRefGoogle Scholar
Howe, R., 𝜃-series and invariant theory, in Automorphic Forms, Representations and L-Functions (Proc. Sympos. Pure Math., Oregon State University, Corvallis, OR, 1977), Part 1, Proceedings of Symposia in Pure Mathematics, Volume XXXIII, pp. 275–285 (1979).Google Scholar
Iwahori, N. and Matsumoto, H., On some Bruhat decomposition and the structure of the Hecke rings of p-adic Chevalley groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 5–48.Google Scholar
Kapranov, M. and Vasserot, E., Vertex algebras and the formal loop space, Publ. Math. Inst. Hautes Études Sci.(100) (2004), 209–269.Google Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne–Langlands conjecture for Hecke algebras, Invent. Math. 87(1) (1987), 153–215.Google Scholar
Lafforgue, V. and Lysenko, S., Geometric Weil representation: local field case, Compos. Math. 145(1) (2009), 56–88.Google Scholar
Laumon, G. and Moret-Bailly, L., Champs Algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, A series of Modern Surveys in Mathematics, Volume 39 (2000).CrossRefGoogle Scholar
Lusztig, G., Singularities, character formulas, and a q-analog of weight multiplicities, in Analysis and Topology on Singular Spaces, II, III (Luminy, 1981), Astérisque, 101, pp. 208–229 (1983).Google Scholar
Lusztig, G., Some examples of square integrable representations of semisimple p-adic groups, Trans. Amer. Math. Soc. 277(2) (1983), 623–653.Google Scholar
Lusztig, G., Affine Hecke algebras and their graded version, J. Amer. Math. Soc. 2(3) (1989), 599–635.CrossRefGoogle Scholar
Lusztig, G., Cells in affine Weyl groups and tensor categories, Adv. Math. 129(1) (1997), 85–98.Google Scholar
Lusztig, G., Bases in equivariant K-theory, Represent. Theory 2 (1998), 298–369 (electronic).Google Scholar
Lusztig, G., Notes on affine Hecke algebras, in Iwahori-Hecke Algebras and their Representation Theory (Martina-Franca, 1999), Lecture Notes in Mathematics, Volume 1804, pp. 71–103. (2002).Google Scholar
Lysenko, S., Geometric theta-lifting for the dual pair SO2m, Sp2n, Ann. Sci. Éc. Norm. Supér. (4) 44(3) (2011), 427–493.CrossRefGoogle Scholar
Mínguez, A., Correspondance de Howe explicite: paires duales de type II, Ann. Sci. Éc. Norm. Supér. (4) 41(5) (2008), 717–741.Google Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166(1) (2007), 95–143.Google Scholar
Mœglin, C., Comparaison des paramètres de Langlands et des exposants à l’intérieur d’un paquet d’Arthur, J. Lie Theory 19(4) (2009), 797–840.Google Scholar
Mœglin, C., Vignéras, M.-F. and Waldspurger, J.-L., Correspondances de Howe sur un corps p-adique, Lecture Notes in Mathematics, Volume 1291 (Springer-Verlag, Berlin, 1987).Google Scholar
Rallis, S., Langlands’ functoriality and the Weil representation, Amer. J. Math. 104(3) (1982), 469–515.Google Scholar
Spaltenstein, N., Classes unipotentes et sous-groupes de Borel, Lecture Notes in Mathematics, 946 (Springer-Verlag, Berlin, 1982).Google Scholar
Srinivas, V., Algebraic K-Theory, 2nd ed., Modern Birkhäuser Classics (Birkhäuser Boston Inc., Boston, MA, 2008).Google Scholar
Waldspurger, J.-L., Démonstration d’une conjecture de dualité de Howe dans le cas p-adique, p≠2, in Festschrift in honor of I. I. Piatetski–Shapiro on the occasion of his 16th birthday, Part I (Ramat Aviv, 1989), Israel Mathematical Conference Proceedings, Volume 2, pp. 267–324 (1990).Google Scholar