No CrossRef data available.
Article contents
INTÉGRALES ORBITALES SUR 
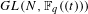$GL(N,\mathbb{F}_{q}((t)))$
Part of:
Lie groups
Published online by Cambridge University Press: 14 May 2019
Résumé
Soit 
$F$ un corps local non archimédien de caractéristique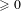 
${\geqslant}0$, et soit 
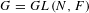$G=GL(N,F)$, 
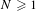$N\geqslant 1$. Un élément 
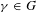$\unicode[STIX]{x1D6FE}\in G$ est dit quasi régulier si le centralisateur de 
$\unicode[STIX]{x1D6FE}$ dans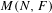 
$M(N,F)$ est un produit d’extensions de 
$F$. Soit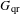 
$G_{\text{qr}}$ l’ensemble des éléments quasi réguliers de 
$G$. Pour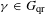 
$\unicode[STIX]{x1D6FE}\in G_{\text{qr}}$, on note 
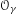$O_{\unicode[STIX]{x1D6FE}}$ l’intégrale orbitale ordinaire sur 
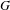$G$ associée à 
$\unicode[STIX]{x1D6FE}$. On remplace ici le discriminant de Weyl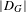 
$|D_{G}|$ par un facteur de normalisation 
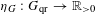$\unicode[STIX]{x1D702}_{G}:G_{\text{qr}}\rightarrow \mathbb{R}_{{>}0}$ permettant d’obtenir les mêmes résultats que ceux prouvés par Harish-Chandra en caractéristique nulle: pour 
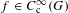$f\in C_{\text{c}}^{\infty }(G)$, l’intégrale orbitale normalisée 
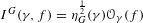$I^{G}(\unicode[STIX]{x1D6FE},f)=\unicode[STIX]{x1D702}_{G}^{\frac{1}{2}}(\unicode[STIX]{x1D6FE})O_{\unicode[STIX]{x1D6FE}}(f)$ est bornée sur 
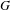$G$, et pour 
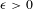$\unicode[STIX]{x1D716}>0$ tel que 
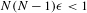$N(N-1)\unicode[STIX]{x1D716}<1$, la fonction 
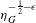$\unicode[STIX]{x1D702}_{G}^{-\frac{1}{2}-\unicode[STIX]{x1D716}}$ est localement intégrable sur 
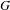$G$.
Abstract
Let 
$F$ be a non–Archimedean local field of characteristic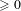 
${\geqslant}0$, and let 
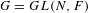$G=GL(N,F)$, 
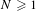$N\geqslant 1$. An element 
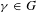$\unicode[STIX]{x1D6FE}\in G$ is said to be quasi–regular if the centralizer of 
$\unicode[STIX]{x1D6FE}$ in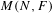 
$M(N,F)$ is a product of field extensions of 
$F$. Let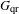 
$G_{\text{qr}}$ be the set of quasi–regular elements of 
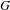$G$. For 
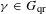$\unicode[STIX]{x1D6FE}\in G_{\text{qr}}$, we denote by 
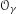$O_{\unicode[STIX]{x1D6FE}}$ the ordinary orbital integral on 
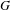$G$ associated with 
$\unicode[STIX]{x1D6FE}$. In this paper, we replace the Weyl discriminant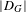 
$|D_{G}|$ by a normalization factor 
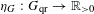$\unicode[STIX]{x1D702}_{G}:G_{\text{qr}}\rightarrow \mathbb{R}_{{>}0}$ which allows us to obtain the same results as proven by Harish–Chandra in characteristic zero: for 
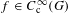$f\in C_{\text{c}}^{\infty }(G)$, the normalized orbital integral 
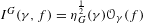$I^{G}(\unicode[STIX]{x1D6FE},f)=\unicode[STIX]{x1D702}_{G}^{\frac{1}{2}}(\unicode[STIX]{x1D6FE})O_{\unicode[STIX]{x1D6FE}}(f)$ is bounded on 
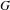$G$, and for 
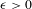$\unicode[STIX]{x1D716}>0$ such that 
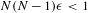$N(N-1)\unicode[STIX]{x1D716}<1$, the function 
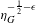$\unicode[STIX]{x1D702}_{G}^{-\frac{1}{2}-\unicode[STIX]{x1D716}}$ is locally integrable on 
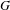$G$.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 2 , March 2021 , pp. 423 - 515
- Copyright
- © Cambridge University Press 2019
Footnotes
L’auteur a bénéficié d’une subvention de l’Agence nationale de la recherche, projet ANR-13-BS01-00120-02 FERPLAY
References
Références
Bushnell, C. et Kutzko, P., The admissible dual of GL (N) via compact open subgroups, Annals Math. Studies, Volume 129 (Princeton University Press, Princeton, New Jersey, 1993).CrossRefGoogle Scholar
Deligne, P., Les corps locaux de caractéristique p comme limites de corps locaux de caractéristique 0, Représentations des groupes réductifs sur un corps local coll., pp. 119–157 (travaux en cours, Hermann, Paris, 1984).Google Scholar
Harish–Chandra, Harmonic analysis on reductive p-adic groups (Notes by G. van Dijk), Lect. Notes Math., Volume 62, pp. 1–125(Springer-Verlag, Berlin-Heidelberg-New York, 1970).Google Scholar
Harish–Chandra, Admissible invariant distributions on reductive p-adic groups, in Lie theories and their applications (Proceedings of the 1977 annual seminar of the Canadian Mathematical Congress, Queen’s University in Kingston, Ontario, 1977)(ed. Rossmann, W.), Queen’s Papers in Pure and Applied Math., Volume 48, pp. 281–347 (Queen’s University, Kingston, Ont., 1978).Google Scholar
Henniart, H., La conjecture de Langlands pour GL (3), Mém. Soc. Math. France (N.S.) 11–12 (1983), 1–186.Google Scholar
Howe, R., The Fourier transform and germs of characters (case of GL
n
over a p-adic field), Math. Ann. 208 (1974), 305–322.CrossRefGoogle Scholar
Jacquet, H. et Langlands, R., Automorphic forms for
$GL(2)$
, Lect. Notes Math., Volume 114, pp. 1–548 (Springer-Verlag, Berlin, 1970).Google Scholar
$GL(2)$
, Lect. Notes Math., Volume 114, pp. 1–548 (Springer-Verlag, Berlin, 1970).Google ScholarKottwitz, R., Harmonic analysis on reductive p-adic groups and Lie algebras, in Harmonic analysis, the trace formula and Shimura varieties (ed. Arthur, J., Ellwood, D. et Kottwitz, R.), Clay Math. Proc., Volume 4, pp. 393–522 (2005).Google Scholar
Lemaire, B., Intégrabilité locale des caractères-distributions de GL (N, F) où F est un corps local non archimédien de caractéristique quelconque, Comp. Math. 100 (1996), 41–75.Google Scholar
Lemaire, B., Intégrales orbitales sur GL (N, F) où F est un corps local non archimédien, Mém. Soc. Math. France 70 (1997), 1–94.Google Scholar
Lemaire, B., Représentations génériques de GL
N
et corps locaux proches, J. Algebra 236 (2001), 549–574.CrossRefGoogle Scholar
Labesse, J.-P. et Waldspurger, J.-L., La formule des traces tordue, d’après le Friday Morning Seminar, CRM Monograph Series, Volume 31 (Amer. Math. Soc., 2013).CrossRefGoogle Scholar
Mœglin, C. et Waldspurger, J.-L., Stabilisation de la formule des traces tordue, Progress in Math., Volumes 316–317, (Springer Int. Pub., 2017).Google Scholar
Repka, J., Shalika’s germs for p-adic GL (n). I. The leading term, Pacific J. Math. 113 (1984), 165–172.CrossRefGoogle Scholar
Repka, J., Shalika’s germs for p-adic GL (n). II. The subregular term, Pacific J. Math. 113 (1984), 173–182.CrossRefGoogle Scholar
Serre, J.-P., Une «formule de masse » pour les extensions totalement ramifiées de degré donné d’un corps local, C. R. Acad. Sc. Paris 286 (1978), 1031–1036.Google Scholar