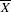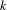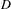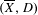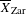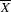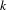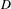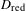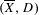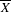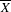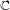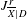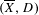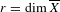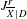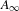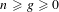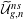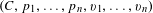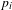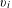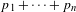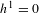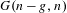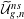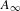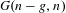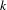We compute the involutive Heegaard Floer homology of the family of three-manifolds obtained by plumbings along almost-rational graphs. (This includes all Seifert fibered homology spheres.) We also study the involutive Heegaard Floer homology of connected sums of such three-manifolds, and explicitly determine the involutive correction terms in the case that all of the summands have the same orientation. Using these calculations, we give a new proof of the existence of an infinite-rank subgroup in the three-dimensional homology cobordism group.

We prove a positive characteristic version of Ax’s theorem on the intersection of an algebraic subvariety and an analytic subgroup of an algebraic group [Ax, Some topics in differential algebraic geometry. I. Analytic subgroups of algebraic groups, Amer. J. Math.94 (1972), 1195–1204]. Our result is stated in a more general context of a formal map between an algebraic variety and an algebraic group. We derive transcendence results of Ax–Schanuel type.

Using recent results by Măcinic, Papadima and Popescu, and a refinement of an older construction of ours, we determine the monodromy action on H^{1}(F(G),\mathbb{C})$H^{1}(F(G),\mathbb{C})$, where F(G)$F(G)$ denotes the Milnor fiber of a hyperplane arrangement associated to an irreducible complex reflection group G$G$.

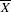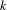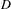Let \overline{X}$\overline{X}$ be a separated scheme of finite type over a field k$k$ and D$D$ a non-reduced effective Cartier divisor on it. We attach to the pair 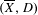(\overline{X},D)$(\overline{X},D)$ a cycle complex with modulus, those homotopy groups – called higher Chow groups with modulus – generalize additive higher Chow groups of Bloch–Esnault, Rülling, Park and Krishna–Levine, and that sheafified on 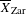\overline{X}_{\text{Zar}}$\overline{X}_{\text{Zar}}$ gives a candidate definition for a relative motivic complex of the pair, that we compute in weight 1$1$. 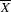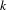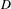When \overline{X}$\overline{X}$ is smooth over k$k$ and D$D$ is such that 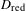D_{\text{red}}$D_{\text{red}}$ is a normal crossing divisor, we construct a fundamental class in the cohomology of relative differentials for a cycle satisfying the modulus condition, refining El Zein’s explicit construction of the fundamental class of a cycle. This is used to define a natural regulator map from the relative motivic complex of 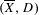(\overline{X},D)$(\overline{X},D)$ to the relative de Rham complex. When 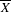\overline{X}$\overline{X}$ is defined over 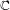\mathbb{C}$\mathbb{C}$, the same method leads to the construction of a regulator map to a relative version of Deligne cohomology, generalizing Bloch’s regulator from higher Chow groups. Finally, when 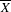\overline{X}$\overline{X}$ is moreover connected and proper over 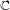\mathbb{C}$\mathbb{C}$, we use relative Deligne cohomology to define relative intermediate Jacobians with modulus 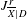J_{\overline{X}|D}^{r}$J_{\overline{X}|D}^{r}$ of the pair 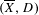(\overline{X},D)$(\overline{X},D)$. For 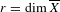r=\dim \overline{X}$r=\dim \overline{X}$, we show that 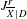J_{\overline{X}|D}^{r}$J_{\overline{X}|D}^{r}$ is the universal regular quotient of the Chow group of 0$0$-cycles with modulus.

In this paper, for each n\geqslant g\geqslant 0$n\geqslant g\geqslant 0$ we consider the moduli stack \widetilde{{\mathcal{U}}}_{g,n}^{ns}$\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ of curves (C,p_{1},\ldots ,p_{n},v_{1},\ldots ,v_{n})$(C,p_{1},\ldots ,p_{n},v_{1},\ldots ,v_{n})$ of arithmetic genus g$g$ with n$n$ smooth marked points p_{i}$p_{i}$ and nonzero tangent vectors v_{i}$v_{i}$ at them, such that the divisor p_{1}+\cdots +p_{n}$p_{1}+\cdots +p_{n}$ is nonspecial (has h^{1}=0$h^{1}=0$) and ample. With some mild restrictions on the characteristic we show that it is a scheme, affine over the Grassmannian G(n-g,n)$G(n-g,n)$. We also construct an isomorphism of \widetilde{{\mathcal{U}}}_{g,n}^{ns}$\widetilde{{\mathcal{U}}}_{g,n}^{ns}$ with a certain relative moduli of A_{\infty }$A_{\infty }$-structures (up to an equivalence) over a family of graded associative algebras parametrized by G(n-g,n)$G(n-g,n)$.

Affine varieties among all algebraic varieties have simple structures. For example, an affine variety does not contain any complete algebraic curve. In this paper, we study affine-related properties of strata of k$k$-differentials on smooth curves which parameterize sections of the k$k$th power of the canonical line bundle with prescribed orders of zeros and poles. We show that if there is a prescribed pole of order at least k$k$, then the corresponding stratum does not contain any complete curve. Moreover, we explore the amusing question whether affine invariant manifolds arising from Teichmüller dynamics are affine varieties, and confirm the answer for Teichmüller curves, Hurwitz spaces of torus coverings, hyperelliptic strata as well as some low genus strata.