Given a compact Lie group 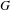 $G$, in this paper we establish
$G$, in this paper we establish 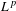 $L^{p}$-bounds for pseudo-differential operators in
$L^{p}$-bounds for pseudo-differential operators in 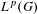 $L^{p}(G)$. The criteria here are given in terms of the concept of matrix symbols defined on the noncommutative analogue of the phase space
$L^{p}(G)$. The criteria here are given in terms of the concept of matrix symbols defined on the noncommutative analogue of the phase space 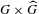 $G\times \widehat{G}$, where
$G\times \widehat{G}$, where 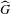 $\widehat{G}$ is the unitary dual of
$\widehat{G}$ is the unitary dual of 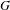 $G$. We obtain two different types of
$G$. We obtain two different types of 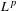 $L^{p}$ bounds: first for finite regularity symbols and second for smooth symbols. The conditions for smooth symbols are formulated using
$L^{p}$ bounds: first for finite regularity symbols and second for smooth symbols. The conditions for smooth symbols are formulated using 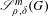 $\mathscr{S}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FF}}^{m}(G)$ classes which are a suitable extension of the well-known
$\mathscr{S}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FF}}^{m}(G)$ classes which are a suitable extension of the well-known 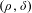 $(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FF})$ ones on the Euclidean space. The results herein extend classical
$(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D6FF})$ ones on the Euclidean space. The results herein extend classical 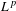 $L^{p}$ bounds established by C. Fefferman on
$L^{p}$ bounds established by C. Fefferman on 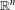 $\mathbb{R}^{n}$. While Fefferman’s results have immediate consequences on general manifolds for
$\mathbb{R}^{n}$. While Fefferman’s results have immediate consequences on general manifolds for 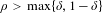 $\unicode[STIX]{x1D70C}>\max \{\unicode[STIX]{x1D6FF},1-\unicode[STIX]{x1D6FF}\}$, our results do not require the condition
$\unicode[STIX]{x1D70C}>\max \{\unicode[STIX]{x1D6FF},1-\unicode[STIX]{x1D6FF}\}$, our results do not require the condition 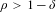 $\unicode[STIX]{x1D70C}>1-\unicode[STIX]{x1D6FF}$. Moreover, one of our results also does not require
$\unicode[STIX]{x1D70C}>1-\unicode[STIX]{x1D6FF}$. Moreover, one of our results also does not require 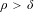 $\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D6FF}$. Examples are given for the case of
$\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D6FF}$. Examples are given for the case of 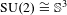 $\text{SU}(2)\cong \mathbb{S}^{3}$ and vector fields/sub-Laplacian operators when operators in the classes
$\text{SU}(2)\cong \mathbb{S}^{3}$ and vector fields/sub-Laplacian operators when operators in the classes 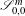 $\mathscr{S}_{0,0}^{m}$ and
$\mathscr{S}_{0,0}^{m}$ and 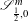 $\mathscr{S}_{\frac{1}{2},0}^{m}$ naturally appear, and where conditions
$\mathscr{S}_{\frac{1}{2},0}^{m}$ naturally appear, and where conditions 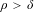 $\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D6FF}$ and
$\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D6FF}$ and 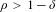 $\unicode[STIX]{x1D70C}>1-\unicode[STIX]{x1D6FF}$ fail, respectively.
$\unicode[STIX]{x1D70C}>1-\unicode[STIX]{x1D6FF}$ fail, respectively.
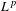 $L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
$L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
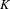 $K$-THEORY OF QUOTIENT SINGULARITIES
$K$-THEORY OF QUOTIENT SINGULARITIES
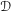 ${\mathcal{D}}$-MODULES
${\mathcal{D}}$-MODULES