Introduction
This study aimed at extending our knowledge about numerical deficits in aphasia. Two relatively neglected issues in this domain were explored: first, what was the extent of the deficit on tasks tapping basic number comprehension, where the verbal component is minimal? Second, how do concomitant numerical deficits might affect activities of daily life?
In order to address such issues, the relation between math and language in the brain should first be briefly considered. In fact, there is strong evidence in the literature indicating that, to a large extent, numerical knowledge and processing are independent of other types of knowledge stored in our brain (e.g., language, memory, etc.). Indeed, according to Delazer, Girelli, Semenza, and Denes (Reference Delazer, Girelli, Semenza and Denes1999), about a quarter of people with aphasia do not show any sign of acalculia, even on complex written calculation tasks.
Basso, Burgio & Caporali (Reference Basso, Burgio and Caporali2000) also showed that aphasia and acalculia may dissociate: 15 out of 34 of their aphasic patients did not show signs of acalculia on the EC301 battery (Deloche et al, Reference Deloche, Seron, Baeta, Basso, Salinas, Gaillard, Vendrell and Stachowiak1993) and some could flawlessly perform a more demanding test of written calculation (Basso & Capitani, Reference Basso and Capitani1979). In an earlier study, Grafman, Passafiume, Faglioni, & Boller (Reference Grafman, Passafiume, Faglioni and Boller1982) showed how calculation disorders, following both left and right hemisphere lesions, are largely independent of other linguistic and nonlinguistic abilities. Rossor, Warrington, & Cipolotti (Reference Rossor, Warrington and Cipolotti1995) reported a case of severe aphasia who answered correctly simple additions, subtractions, and multiplications. The patient also performed multidigit operations without problems.
Varley, Klessinger, Romanowski, & Siegal (Reference Varley, Klessinger, Romanowski and Siegal2005), by analyzing in detail the performance of three patients with extensive perisylvian lesions, found that, notwithstanding severe grammatical problems and difficulties in processing words, these patients did not show calculation difficulties. All these patients could correctly solve equations and arithmetical problems. Patients with a severe progressive aphasic condition, like semantic dementia, are impaired in naming, reading, writing of non-number words; impairment is present also on several other verbal and visual tasks (Cappelletti, Butterworth, & Kopelman, Reference Cappelletti, Butterworth and Kopelman2001). Nevertheless, patients with semantic dementia may show virtually no deficit with numbers and calculation (Cappelletti, Kopelman, Morton, & Butterworth, Reference Cappelletti, Kopelman, Morton and Butterworth2005; Crutch, & Warrington, Reference Crutch and Warrington2002; Diesfeldt, Reference Diesfeldt1993; Julien, Thompson, Neary, & Snowden, Reference Julien, Thompson, Neary and Snowden2010; Zamarian, Karner, Benke, Donnemiller, & Delazer, Reference Zamarian, Karner, Benke, Donnemiller and Delazer2006).
Severe disorders of numerical functions, on the other hand, maybe independent of language problems. Cipolotti, Butterworth, & Denes (Reference Cipolotti, Butterworth and Denes1991) described case CG, who sustained left parietal damage. Except for reading and writing, CG remained very proficient on language tasks as well as on reasoning tasks. Furthermore, CG retained a normal IQ. Yet, she could not process, verbally or otherwise, numbers larger than four. Similar cases were reported by Delazer, Karner, Zamarian, Donnemiller, & Benke (Reference Delazer, Karner, Zamarian, Donnemiller and Benke2006), Warrington (Reference Warrington1982), and Denes, & Signorini (Reference Denes and Signorini2001).
Language and math may share, nonetheless, some resources depending on the nature of the tasks. For example, some tasks may require, selective attention, attention to space, or visuospatial processing (see Granà, Hofer & Semenza, Reference Granà, Hofer and Semenza2006 for a discussion about these last cases). Elements of acalculia appear to be associated with aphasia because of anatomical contiguity of separate functions or because of the nature of the task (Deloche & Seron, Reference Deloche and Seron1982; Seron & Deloche, Reference Seron and Deloche1983).
Of relevance to the present investigation, some math tasks are believed to be verbal in nature. Failure on such tasks would be determined by the disruption of a cognitive component shared by the language and the math systems. A typical example of this is arithmetical table retrieval. In the influential model of Dehaene & Cohen (Reference Dehaene and Cohen1995), in fact, retrieval of overlearned and rote memorized arithmetical tables, is assimilated to naming, and is carried out with the critical contribution of the left angular gyrus, just as the retrieval of words. Recent studies on this matter, however (Della Puppa et al. Reference Della Puppa, De Pellegrin, D’Avella, Gioffrè, Munari, Saladini and Semenza2013; Semenza et al., Reference Semenza, Salillas, De Pallegrin and Della Puppa2017; Semenza and Benavides-Varela, Reference Semenza and Benavides-Varela2017; Salillas et al, Reference Salillas, Piccione, Di Tomasso, Zago, Arcara and Semenzain press), have shown that even solving arithmetical tables requires a complex system with the crucial contribution of the right hemisphere.
Number transcoding also includes verbal numerical tasks such as reading aloud and writing number words. On these tasks, Deloche and Seron (Reference Deloche and Seron1982) and Seron and Deloche (Reference Seron and Deloche1983) compared error types in Broca’s and in Wernicke’s aphasia. They found that Broca’s aphasics, who have syntactic problems, tend to make “syntactic errors”. In syntactic errors, violations occur of the order of magnitude, that spare the correct lexical elements: they are made when the power of 10 is wrong with respect to the target. These errors may thus result in longer or shorter numbers (e.g., 36/360). In contrast, Wernicke’s aphasics, who have problems with the choice of words, tended to commit “lexical errors”. Lexical errors consist of the incorrect production of one or more of the individual elements in a number, leading to the production of a number of the same magnitude (e.g., 36/24). The authors concluded that, since number processing deficits in Broca’s and Wernicke’s aphasics looked parallel to their language deficits, there was ground to believe that their errors resulted from damage to shared cognitive components.
Anatomically, it is believed that most math and language abilities have their origin in the same hemisphere. In this respect, Semenza et al. (Reference Semenza, Delazer, Bertella, Granà, Mori, Conti and Mauro2006) studied mathematical abilities in cases of “crossed aphasia”. In this rare condition, aphasia in right-handed individuals follows lesions of the right hemisphere, instead of lesions of the left hemisphere. Semenza et al. (Reference Semenza, Delazer, Bertella, Granà, Mori, Conti and Mauro2006) found that, in a series of cases with crossed aphasia, involving frontal, parietal, and/or temporal lesions, acalculia was always present. Moreover, for each case, the pattern of errors was similar to that previously observed in the most common types of aphasias resulting from left hemisphere lesions (e.g., in Delazer et al., Reference Delazer, Girelli, Semenza and Denes1999). No sign of spatial acalculia (a type of acalculia resulting from right hemisphere damage in left-lateralized right-handed subjects) was detected. Thus, Semenza et al. (Reference Semenza, Delazer, Bertella, Granà, Mori, Conti and Mauro2006) suggested that numerical and linguistic abilities are implemented within the same hemisphere. Pinel & Dehaene (Reference Pinel and Dehaene2010) provided converging neuroimaging evidence for such conclusions, adding further neuroanatomical data to what appears to be a very complex relation, implying a myriad of different structures and corresponding tasks.
In summary, studies exploring the relation between math and language in the brain suggest that such relation is conditioned by the highly modular functional and anatomical organization of both systems, whereby areas of overlapping coexist with areas that are functionally independent. The clinical result of damage to such systems is bound to be complex and extremely variable, as it has been already widely described (Basso, Burgio & Caporali, Reference Basso, Burgio and Caporali2000; Cipolotti & van Harskamp, Reference Cipolotti, van Harskamp and Berndt2001; Semenza, Reference Semenza, Stemmer and Whitaker2008; Cappelletti, Reference Cappelletti, Cohen Kadosh and Dowker2015; Salillas & Semenza, Reference Salillas, Semenza, Cohen Kadosh and Dowker2015).
Gaining general knowledge about whether a deficit in basic number comprehension tasks is present in aphasia may pave the way to reinforce rehabilitation attempts by considering such tasks in training. We tried to offer some speculations and hope our investigation might reveal how much difficulty a given individual with aphasia can experience in Numerical Activities of Daily Living (NADL), and in which particular domain. It is important to provide a more organized path for the patient and attempt to reinsert this individual in a profitable quality of life.
In light of the above considerations, we thus explored numerical deficits in individuals with aphasia, contributing further to widen our knowledge in a direction that has not been updated in recent years. For the first time, we specifically investigated whether numerical deficits, usually accompanying aphasia, can be observed on number comprehension tasks that do not require an oral response. Three such tasks were administered in this investigation (for a full description, see later in the Method section): Numerosity Comparison, Number Line Marking, and Digit Comprehension. In these tasks, stimuli are simultaneously presented to the participant. Numerosity comparison has been used with nonhuman species, and therefore does not require language (see Butterworth, Reference Butterworth, Bartolini Bussi and Sun2018; Dehaene, Reference Dehaene2011). Number Line Marking and Digit Comprehension do not necessarily require language: understanding digits, however, is usually learned after learning the names of numbers; lexical access may then be required. The first two of these tasks are used to evaluate the approximate number system. All the three tasks are likely to be failed in right hemisphere lesions (Benavides-Varela et al., Reference Benavides-Varela, Piva, Burgio, Passarini, Rolma and Semenza2017), but do left hemisphere lesions causing aphasia affect these tasks as well.
Furthermore, we examined the impact of aphasia on NADL. The way we pursued this exploration profits from the availability of NADL (Semenza et al., Reference Semenza, Meneghello, Arcara, Burgio, Gnoato, Facchini and Butterworth2014), a relatively easy to administer battery that encompasses basic number comprehension tasks and investigates a number of activities of daily living. All NADL investigations to date were not aimed at obtaining information about known math deficits in aphasia, nor on their anatomical location.
These questions are independent of the variability of the possible type of difficulties in individuals with aphasia. They are also independent of the severity of such deficits, regarding the co-occurrence of number comprehension problems and the impact of math problems on activities of daily living. In order to answer the abovementioned questions, tasks were employed that were never previously used in the aphasia literature, but that are thought to be important for clinical purposes.
This way we aimed at the same time to the validation process of the NADL for the Greek population as well as starting to examine the influence of gender, age, and education on performance on the NADL.
Method
Participants
Sixty-six participants, 31 female and 35 males, between the ages of 25 and 87 (mean = 58.06, SD = 16.47), from various regions of northern Greece, took part in the study. Thirty three were healthy, control participants, with no record of previous vascular incidents, traumatic brain injuries, and tumors or other developmental, neurological, or psychiatric disorders (17 females and 16 males; mean age = 56.39, SD = 14.94; mean education years = 11.36, SD = 4.66). Thirty-three participants were individuals diagnosed with aphasia (14 females and 19 males; mean age = 57.9, SD = 20.54; mean education years = 11.30, SD = 5.90). In regard to the etiology, aphasia emerged from left side ischemic cerebrovascular stroke (n = 18, 54.5%), from TBI (n = 6, 18.2%), from left side tumor (n = 3, 9.1%), from left side ischemic hemorrhagic stroke (n = 3, 9.1%), from viral damage ( = 2, 6.1%), and from basal ganglia damage (n = 1, 3.0%).
All individuals with aphasia were inpatients of the Anagennisi (Revival) Physical Recovery and Rehabilitation Centre (Thessaloniki, Greece, approval number # 368-2018) as well as of the AHEPA University Hospital (Thessaloniki, Greece). The criteria related to the decision-making process on admission as an inpatient to a private and a public stroke rehabilitation unit were both based on medical and clinical factors (Putman et al., Reference Putman, De Wit, Schupp, Beyens, Dejaeger, De Weerdt and Leys2007). The minimum and maximum times post onset of illness were 28 days and 48 months, respectively (mean time = 9.15, SD = 12.40 months).
Thirty-three control participants were initially recruited to match the patients, giving approximately a 1:1 ratio of patients and controls (Raina, Reference Raina2014), and were selected from the general population of Katerini, Kastoria, Serres, and Thessaloniki (Greece). The results of independent samples t test showed that individuals with aphasia and controls did not differ significantly by age [t(63) = −0.827, p = .411] or education [t(61) = −0.914, p = .364]. All the participants were native Greek speakers. They were informed about the study and signed a consent form. Their well-being and confidentiality were protected by the researchers and testing took place in accordance with the ethical guidelines of the 1964 Declaration of Helsinki and its later amendments or comparable ethical standard.
Patients were classified according to lesion site and not based on the basis of aphasic symptoms. Some categories (e.g., Wernicke’s and Conduction) included only a few patients, leading to difficulties in analysis and inferences. Thus, we decided to collapse the data into three groups based on location of the lesion rather than on the classic category: Anterior (including Broca; mean age=67.00, SD=14.68), Posterior (including Wernicke, Anomic, and Conduction; mean age=51.15, SD=18.96), and Global (mean age=44.0, SD=32.99). The lesions’ location for the three groups was, thus, further checked to see whether and was evaluated using CT scans and MRI, by neuroradiologists who were unaware of the purposes of this study.
No cases were found in whereby the bulk of the lesion was not as traditionally expected (all Broca’s aphasics had an anterior lesion while the other individuals, except Global aphasics, had a posterior lesion). Cases with bilateral or multiple lesions were excluded from the study. We finally recruited 33 individuals with aphasia as their primary diagnosis.
An even more compelling reason to classify patients on the basis of lesions’ location was the lack of homogeneity in available clinical data, in our sample. Clinical data, in fact, were collected for clinical purposes only, from several different labs, hospitals, and rehabilitation centers and, thus, different assessment protocols were used. In fact, 25 individuals with aphasia were given the Cookie Theft picture description task, from the Boston Diagnostic Aphasia Examination (BDAE) (Tsapkini, Vlahou, & Potagas, Reference Tsapkini, Vlahou and Potagas2010) (range: 0–5) and scored a mean of 2.28 (SD=1.72). Nineteen individuals with aphasia were given the Greek standardized version of the Boston Naming Test (BNT) (Patricacou, Psallida, Pring, & Dipper, Reference Patricacou, Psallida, Pring and Dipper2007) (range: 0–15), with mean score of items answered correctly 7.00 (SD=4.63). A wide variety of other diagnostic tests, moreover those assessing comprehension, were each administered to an even smaller proportion of the entire sample.
We were positive that all instructions were given in a clear and concise way and when necessary, the investigators checked back with each individual with aphasia, even for the individuals with Global aphasia, rewording instructions and giving visual, tactile cues, so that they were clear to the participants before administering the tests. Patients were allowed to take a break whenever they felt fatigued and the investigator continued after the patient was rested.
Materials and Procedure
Numerical abilities were measured with the NADL battery (see Semenza et al., Reference Semenza, Meneghello, Arcara, Burgio, Gnoato, Facchini and Butterworth2014 for a full description and downloading). The NADL, now widely used for clinical and experimental purposes, assesses both numerical abilities acquired during school years (in the “formal part”) and the impact of possible numerical difficulties on participants’ everyday life (in the “informal” part). The NADL consists of two separate sections, the formal and the informal one. Scores are provided for each section separately.
The formal part of the NADL includes traditional numerical tasks such as reading and writing of numbers, mental calculation, written rules and principles, and written operations. All 12 subtests from the formal part of the NADL were analyzed. These included (1) Numerosity comparison, (2) Number Line Task, (3) Digit Comprehension, (4) Reading Arabic Numerals, (5) Writing Arabic Numerals to Dictation, (6) Mental Calculation of Addition, (7) Mental Calculation of Subtraction, (8) Mental Calculation of Multiplication, (9) Written Rule Comprehension, (10) Written Principles Addition, (11) Written Principles Multiplication, and (12) Written Operations (addition, subtraction, multiplication) (see Semenza et al., Reference Semenza, Meneghello, Arcara, Burgio, Gnoato, Facchini and Butterworth2014 for more details). Relevant for the aims of the present investigation, NADL also includes three subtests that do not necessarily require verbal abilities: (a) Number Comparison, in which the participant is asked to compare the number of squares in two panels presented simultaneously (up to nine squares per panel); (b) Number Line Marking, where the participant is asked to mark a given number on a line defined by its end points (e.g., where it is 75 in a 0–100 interval line); (c) Digit Comprehension, where panels are presented, similar to those described in (a), one at a time along with a list of digits 1–10; the participant is asked to point to the appropriate digit corresponding to the number of squares on each panel. The informal part of the NADL assesses the numerical competence likely to be necessary for everyday life. It encompasses questions in the domains of Time (current date?), Measure (amount of pasta or rice in an average portion?), Transportation (distance between home and hospital?), Communication (own telephone number?), General Knowledge (days in a week?), and Money (cost of a car?).
There was a standard “forward-backward” translation procedure from Italian to Greek by a team of two healthcare clinicians who knew both languages and was then checked by one of the co-authors, who is bilingual in Italian and Greek. This was done in order to examine the quality of the translation.
The NADL was administered following the assessment using Cookie Theft and the BNT in a single session. Due to the clinical environment and time allocated regulations the researcher had with all subjects, no further cognitive testing was completed. All participants were tested individually and in a quiet and private room. During the sessions, written notes were taken and subsequently analyzed, in order to score correctly the participants’ performance. The administration of the NADL battery lasted 25–50 min, depending on aphasia severity. The battery was always administered in the following order: participant interview, assessing participants’ awareness about their numerical deficit (e.g., “Do you get confused by numbers?”; for more information, see Semenza et al., Reference Semenza, Meneghello, Arcara, Burgio, Gnoato, Facchini and Butterworth2014), followed by the informal test and then by the formal test.
As this is a preliminary analysis in attempts to begin the standardization process for the Greek version of NADL, we first had to make an investigation on the normative data from individuals with aphasia and healthy controls. At the present stage of this work, we used the original spreadsheet, from the Italian language translated to the Greek language, as a guide to conduct the research. Once the assessment process was over, participants’ scores were transcribed into the spreadsheet, which automatically classified their scores into normal or impaired categories based on an algorithm. This algorithm takes into account demographic variables as well, i.e., gender, age, and educational level of the participant, and is based on the predicted scoring a typical person would obtain. Below a cutoff, the performance of the participants is considered impaired.
We performed frequentist analyses with IBM SPSS Statistics 25 (IBM, Armonk, NY, USA) and effect sizes and Bayesian analyses with JASP (Version 0.11.1). We conducted multiple linear regressions to investigate the relation between demographic factors and the performance of individuals with aphasia, on the NADL. Furthermore, we performed a series of independent samples t tests and one-sample t tests to compare the performance of individuals with aphasia and that of healthy controls, on the NADL (total score and subtests; separately for the formal and the informal part). To control for violations of homoscedasticity, we reported the Welch correction (independent samples t tests). To control for violations of normality, we also reported nonparametric analyses. We calculated Cohen’s d for classic t tests (for the formula used in JASP, see https://forum.cogsci.nl/discussion/3013/what-denominator-does-the-cohens-d-use-on-jasp). Furthermore, to tackle some limits of the classic Cohen’s d, when SD is close to 0, we also calculate Cohen’s d for the robust Welch t test. In addition, to further control for the limits of the classic Cohen’s d, we also calculated effect sizes for all the nonparametric analyses. In addition, confidence intervals (95%) were reported for all the analyses. Finally, we calculated the Bayes factor (BF) for each analysis (for guidelines on BFs, see Wagenmakers, Love et al., Reference Wagenmakers, Love, Marsman, Jamil, Ly, Verhagen and Morey2018; Wagenmakers, Marsman et al., Reference Wagenmakers, Marsman, Jamil, Ly, Verhagen, Love and Morey2018). Blending Bayesian and Frequentist methods can give complementary bits of information given that different aspects of statistical inference are tackled (e.g., Bayarri & Berger, Reference Bayarri and Berger2004). For instance, if the two approaches go toward the same direction, researchers can be more confident about the robustness of their findings (e.g., Aleotti et al., Reference Aleotti, Di Girolamo, Massaccesi and Priftis2020).
Results
Formal Part of the NADL
Relation between demographic factors (age, education, and gender) and the total score
We first ran an exploratory analysis on the effect of age, education, and gender on the total score of the formal part of the NADL. Only education was a significant predictor (see supplemental data).
Analyses on the Total Score
Individuals with aphasia versus healthy controls
On the total score, the performance of individuals with aphasia (M = 39.727, SD = 24.352) differed significantly from that of healthy controls (M = 68.515, SD = 10.214; see Table 1). Cohen’s d for the parametric analyses revealed a strong effect (1.512). Finally, the BF showed the presence of extreme evidence for the difference (BF10 = 285456.528, error % = 4.109e-8).
Table 1. Formal part: performance comparison between individuals with aphasia and healthy controls

For the Student’s t test and Welch t test, location parameter is given by mean difference; for the Mann–Whitney test, location parameter is given by the Hodges–Lehmann estimate.
For the Mann–Whitney test, effect size is given by the rank biserial correlation. For the other test(s), by Cohen’s d.
Analyses on the subtests (individuals with aphasia versus healthy controls)
We performed a series of independent-samples t tests for most of the subtests (i.e., 12 subtests). For the subtests “Numerosity comparison” and “Mental calculation of addition”, the performance of healthy controls was constant (i.e., all healthy participants scored “6”). Therefore, we performed two one-sample t tests against the score “6”. The performance of healthy controls significantly differed from that of individuals with aphasia on all the 14 subtests of the formal part of the NADL (see Tables 1 and 2). Note that all significant differences remained the same (i.e., all ps < .05) even after correcting with False Discovery Rate (not reported). Effect sizes and BFs are considered successively (Tables 1 and 3).
Table 2. Performance comparison between individuals with aphasia and healthy controls on the 14 subtests of the NADL (formal part)

For the Student’s t test and Welch t test, location parameter is given by mean difference; for the Mann–Whitney test, location parameter is given by the Hodges–Lehmann estimate.
For the Mann–Whitney test, effect size is given by the rank biserial correlation. For the other test(s), by Cohen’s d.
a The variance in Numerosity Comparison is equal to 0 after grouping on Aphasic and Nonaphasic.
b The variance in Mental Calculation of Addition is equal to 0 after grouping on Aphasic and Nonaphasic.
Table 3. NADL formal subtests: Means and standard deviations of the performance of individuals with aphasia and healthy controls

Independent samples t tests (effect sizes and BF)
Cohen’s d revealed the presence of strong effects (range: 0.777–1.648; Table 2). Finally, the BFs showed the presence of strong to extreme evidence for the differences (BF range: 14.628–236612.378; Table 3).
One-sample t tests (effect sizes and BF)
For the “Numerosity comparison” subtest, Cohen’s d revealed a rather strong effect (−0.741; Table 2). The BF, however, showed moderate evidence against the difference (BF = 0.256, error % = 2.063e-6; Table 4). For the “Mental calculation of addition” subtest, Cohen’s d revealed a strong effect (−0.919; Table 2). The BF showed the presence of moderate evidence for the difference (BF = 8.477, error % = 6.036e-7; Table 4).
Table 4. NADL formal subtests: Bayesian factors (individuals with aphasia vs. healthy controls)

Informal part of the NADL
Relation between demographic factors (age, education, and gender) and the total score
We first ran an exploratory analysis on the effect of age, education, and gender on the total score of the informal part of the NADL. Only education was a significant predictor (see supplemental data).
Analyses on the total score
Individuals with aphasia versus healthy controls
On the total score, the performance of individuals with aphasia (M = 12.818, SD = 7.139) differed significantly from that of healthy controls (M = 20.970, SD = 2.675; see Table 5). Cohen’s d for the parametric analyses revealed a strong effect (1.512). Finally, the BF showed the presence of extreme evidence for the difference (BF10 = 183807.530, error % = 3.916e-10).
Table 5. Informal part: performance comparison between individuals with aphasia and healthy controls

For the Student’s t test and Welch t test, location parameter is given by mean difference; for the Mann–Whitney test, location parameter is given by the Hodges–Lehmann estimate.
For the Mann–Whitney test, effect size is given by the rank biserial correlation. For the other test(s), by Cohen’s d.
Analyses on the subtests (individuals with aphasia vs. healthy controls)
We performed a series of independent samples t tests for all the subtests, except for the subtest “Transportation”. In this subtest, the performance of individuals with aphasia was constant (i.e., all patients scored “0”). Therefore, we performed a one-sample t test against the score “0”. The performance of individuals with aphasia significantly differed from that of healthy controls on all the subtests of the informal part of the NADL, except for Measurement (see Tables 6 and 7). Note that all significant differences remained the same (all ps < .05) even after correcting with False Discovery Rate (not reported). Effect sizes and BFs are considered successively.
Table 6. Performance comparison between individuals with aphasia and healthy controls on the seven subtests of the NADL (informal part)

For the Student’s t test and Welch t test, location parameter is given by mean difference; for the Mann–Whitney test, location parameter is given by the Hodges–Lehmann estimate.
For the Mann–Whitney test, effect size is given by the rank biserial correlation. For the other test(s), by Cohen’s d.
a The variance in Transportation is equal to 0 after grouping on Aphasic and Nonaphasic.
Table 7. NADL informal subtests: Means and standard deviations of the performance of individuals with aphasia and healthy controls.

Independent samples t tests (effect sizes and BF)
Cohen’s d revealed the presence of strong effects for all significant differences (range: 1.012–1.383; Table 6). Finally, the BFs showed the presence of extreme evidence for the differences (BF range: 14.628-236612.378; Table 8).
Table 8. NADL informal subtests: Bayesian factors (individuals with aphasia vs. healthy controls).

Impairments on NADL
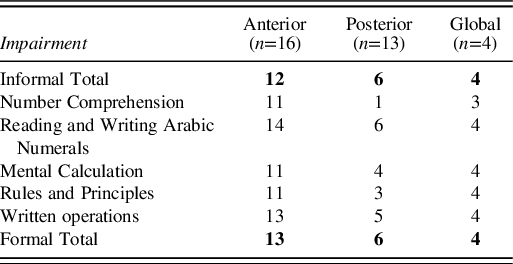
Impairment or non-impairment in total scores of informal and formal parts, as well as the subtests included, is depicted in Table 9. It is possible to observe that almost all Global patients presented deficits in every task. Comparing the performance between Anterior and Posterior, the latter performed significantly better than the former.
Table 9. Failure/success for each individual was determined on the basis of the NADL scoring system and database.
Error Analysis
As shown in Table 10, for the “Reading numbers aloud” and “Writing numerals on dictation tasks”, errors were classified as lexical, syntactic, mixed, or omission (Delazer et al., Reference Delazer, Girelli, Semenza and Denes1999). Lexical errors consisted of substitutions of single elements of the numbers that belong to the same lexical class (e.g., 3 → 2 or 4, or 11 → 10 or 12). These errors have also been called position-within-class errors. Syntactic errors concern the syntactic structure of the numeral (e.g., 12 → 2; 105 → 1005). Additional classes consisted of mixed errors (substitution of elements in syntactically wrong numbers) and omissions. Both in the “Reading numbers aloud” and “Writing numerals on dictation” tasks, anterior aphasics made more errors, whereas posterior aphasics gave mainly correct answers and global aphasics could not complete the tasks.
Table 10. Raw error counts of individuals with aphasia in formal subtests

Table 10 illustrates the errors made in the “Mental Calculation”, “Written Rules and Principles”, and “Written Operations” tasks, classified as procedural, calculation, mixed, and omissions (Delazer et al., Reference Delazer, Girelli, Semenza and Denes1999). Procedural errors consisted of failure with the sequential steps needed to carry out the multidigit calculation. Typical errors of this type include failures in using the carry-over procedure during addition (e.g., 14 + 7 = 11), the borrowing during subtraction or the selection of the correct factors during multiplication. Calculation errors, on the other hand, consisted of failure to answer the single problems within complex calculation (e.g., 5 + 3 = 6). Mixed errors included both procedural and calculation errors and omissions were also counted. In the “Mental Calculation” and “Written Calculation” tasks, anterior aphasics made in general the most errors, including omissions. In the “Written Operations task”, anterior aphasics made fewer procedural errors than posterior aphasics, but more calculation errors than omissions. Global aphasics made 74 omissions. This finding demonstrates that global aphasics tried to solve the mathematical operations, but they were unable to give a specific final answer.
Discussion
The current findings confirm what is reported in the literature (Grafman et al, Reference Grafman, Passafiume, Faglioni and Boller1982; Jackson, & Warrington, Reference Jackson and Warrington1986; Rosselli, & Ardila, Reference Rosselli and Ardila1989; Delazer et al., Reference Delazer, Girelli, Semenza and Denes1999; Basso et al., Reference Basso, Burgio and Caporali2000) insofar as the results show that most people with aphasia have a concomitant acalculia. Also consistent with previous literature is the finding, revealed by the inspection of individual participants’ performance, that aphasia does not necessarily impair mathematical abilities. In fact, for each task, a number of individuals in both the anterior and the posterior group performed within normal limits. Not surprisingly, for individuals with global aphasia, where the lesion was larger, a concomitant acalculia, affecting almost invariably all tasks, was shown for each participant.
This study shows, for the first time, that problems with number comprehension tasks are likely to accompany the aphasic condition. Indeed, with respect to controls, the performance of individuals with aphasia was significantly impaired also on Number Comparison, Number Line Marking, and Digit Comprehension. These tasks are widely used to assess math abilities in preschool children and are believed to be predictive of success in math learning (Benavides-Varela et al., Reference Benavides-Varela, Passarini, Butterworth, Rolma, Burgio, Pitteri and Semenza2016). The fact that numerical deficits in some people with aphasia may extend to such tasks shows how deep the math deficit for that individual may be kept relevant to those who are trying to improve rehabilitation. Further research may eventually reveal the efficacy of training number comprehension tasks to recuperate efficient dealing with math. Likewise, it may be interesting to extend future investigations to tasks that are not encompassed in NADL, such as quantity evaluation (De Luccia & Zazo Ortiz, Reference De Luccia and Zazo Ortiz2016).
Importantly, people with aphasia are very likely to have difficulties in a wide range of NADL. Consistently with the literature, this study, in fact, revealed difficulties in almost all of the domains considered in NADL (i.e., Time, Transportation, Communication, General Knowledge, and Money; the only exception being Measurement). This finding was highly supported, not only by traditional frequentist analyses (both parametric and nonparametric) and by effect sizes, but also by BFs supporting the presence of extreme evidence (i.e., BFs > 100) for the differences between individuals with aphasia and control participants.
In light of such results, the question may arise about to what extent specific deficits in mathematical abilities can be directly attributed to specific aphasic deficits or just to the overall presence of a brain lesion (wherever located) and determined generically by the severity of such lesion. Indeed, one may wonder whether there is a causal relation between the presence of a specific linguistic deficits and specific mathematical difficulties. However, it must be noted that the previous literature reporting mathematical deficits in group studies with sample sizes comparable to the one in the present investigation, and even where full clinical data were available, did not go much further in this direction either. For example, the most representative of such studies, Delazer et al. (Reference Delazer, Girelli, Semenza and Denes1999), concluded that, although the findings suggested associations between impairments in language processing and impairments in numerical tasks, drawing conclusions on the verbal basis of numerical tasks was to be taken with caution. This conclusion, they argue, can only be mitigated by the intuition that some functions (like table retrieval) might be preferentially supported by linguistic functions. On this matter, therefore, one may wonder whether a group study of this sort could ever provide grounds for more definitive conclusions on the basis of correlations, especially considering the fact that language and numerical abilities have been shown to dissociate.
Where Delazer et al. (Reference Delazer, Girelli, Semenza and Denes1999) did, however, find useful information was in the analysis of errors. Qualitative differences between groups in the production of errors may in fact reflect specific, rather than generic, difficulties. In number transcoding, they found a larger proportion of “syntactic” errors in Broca’s aphasia rather than in Wernicke’s aphasics. In contrast, they found the opposite pattern with “lexical” errors: Wernicke’s aphasics were more impaired than Broca’s aphasics. This pattern was consistent with earlier aforementioned findings from Seron, & Deloche, Reference Seron and Deloche1983. Basso, Burgio & Caporali (Reference Basso, Burgio and Caporali2000), however, had found a somewhat different pattern: syntactic errors were the most frequent type of error in both groups (i.e., Broca’s and Wernicke’s aphasics), although syntactic errors were found in a larger proportion in Broca’s aphasics.
Interestingly, number transcoding errors have been reported also in right hemisphere patients. In the large majority, however, in right hemisphere lesions, transcoding errors affect complex numbers containing zero (Benavides-Varela et al., Reference Benavides-Varela, Passarini, Butterworth, Rolma, Burgio, Pitteri and Semenza2016; Reference Benavides-Varela, Piva, Burgio, Passarini, Rolma and Semenza2017), thus, showing that brain damage affects number transcoding depending on the site of lesion and on the specific function sustained by the damaged area. In the present study, anterior aphasic patients made comparatively more syntactic errors than the posterior aphasic patients. However, the lexical errors were similar for both groups. For mental calculation, calculation errors were preponderant over procedural errors for both anterior and posterior aphasics groups, while the reverse pattern was observed in written calculation. In written operations, anterior aphasics made more calculations than procedural errors in contrast to posterior aphasics whose answers yielded the opposite error pattern. This last finding, consistent with Delazer et al. (Reference Delazer, Girelli, Semenza and Denes1999), may reveal that memory for arithmetical calculation procedures may be stored in posterior areas.
The question of specificity may also be asked in relation to the tasks, central in the present investigation, that were not administered to aphasics in previous literature (i.e., NADL comprehension tasks and everyday life tasks). Here, we can only compare the present findings with those of Benavides-Varela et al. (Reference Benavides-Varela, Piva, Burgio, Passarini, Rolma and Semenza2017) in right-sided lesions. In this study, errors in the comprehension tasks were all spatial in nature. As far as NADL are concerned, right hemisphere patients differed from controls only in the total score, while showing a tendency in time estimation and money usage. Our aphasic sample showed a more severe deficit than the control group in all daily life aspects except for measurement. This finding supports the fact that individuals with aphasia, in general, have difficulty with most numerical activities in everyday life.
Education seems to have a protective role in both formal and everyday life mathematical abilities in the presence of aphasia (see supplemental data). This is consistent with what has been found in other studies (e.g., Arcara et al., Reference Arcara, Mondini, Bisso, Palmer, Meneghello and Semenza2017) assessing the role of education in protecting mathematical abilities in the elderly population. In contrast, gender, and, somehow surprisingly, age does not seem to modulate the severity of acalculia, which must therefore largely depend on factors like the size and location of the lesion. No data were available on these issues so far in previous literature.
Conclusion
The current study uses only 33 individuals with aphasia, as a preliminary investigation. Our paper paves the way for future empirical experimentation using the NADL. The limitations of the present study include the following: critically, the lack of detailed data about each patient’s manifold linguistic deficits surely permits only a tentative answer to this question. Furthermore, we acknowledge that the lack of consistent language comprehension tests used across all participants may restrict research evidence as well.
Notwithstanding these shortcomings, a number of important, safe, conclusions could be reached. This study shows that the problems which an aphasic patient may experience in number comprehension tasks and activities of daily living may not be negligible. Both deficits may seriously contribute to limiting a person with aphasia capacity to deal with numbers and live as a numerate citizen. In practice, the assessment and rehabilitation of mathematical disorders are not part of the routine therapy for aphasia. Nonetheless, speech therapy and/or neuropsychological rehabilitation can be a demanding enterprise and we hope this work will provide some insight regarding aspects of acalculia that, at least in part, establishes a new framework for including the assessment and the rehabilitation of acalculia as part of routine speech therapy and/or neurorehabilitation for aphasia. We also expect that this study will motivate future research that will consider the effects of both numerical activities in everyday life and mathematical abilities and will further investigate whether there are any mutual interactions.
Studies like the present one, despite its shortcomings, provide sufficient evidence to clearly make a case for the insertion of mathematical abilities assessment, such as the NADL, for the generation of a unitary clinical diagnostic instrument, which could be of interest to clinicians in Greece and could also be used for cross-linguistic comparisons.
Acknowledgments
The authors would like to thank Evgenia-Peristera Kouki, Freideriki Tselekidou, and Sophia Tigka for data collection and the Anagennisi (Revival) Physical Recovery and Rehabilitation Centre (Thessaloniki, Greece) as well as everybody who participated in the study.
Ethics Statement
All participants were informed about the aims of the investigation and participated voluntarily and gave their informed written consent. The data were obtained in compliance with the Helsinki Declaration for Human Research.
Financial Support
The authors have no financial disclosures to report.
Conflict of Interest
The author(s) have nothing to disclose.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S1355617720001368.











