1 Introduction
Sports is a domain that has grown significantly over the last 20 years to become a key driver of many economies, while at the same time, impacting on our social and cultural fabric. According to a recent reportFootnote 1, the estimated size of the global sports industry is $1.3 trillion and has an audience of over 1 billion, who may attend matches to support their favourite teams, bet in various online or offline markets, or watch games on the television for pure entertainment. Sports employ over 1 million jobs in the UK alone, with those involved either playing games, managing teams, or looking after the health and fitness of players. At the core of these economic and social impacts, are the individuals, players, and teams involved. Indeed, as we will demonstrate in this paper, predicting and optimizing the performance in sports are challenging problems but, so far, such problems have largely been dealt with by domain experts (e.g., coaches, managers, scouts, and sports health experts) with basic analytics. Specifically, we focus on team sports as they present the most difficult challenges and tend to have the greatest audience and economic benefit.
We define a team sport as a game that typically involves two teams playing against each other, each composed of a set of players with their individual roles and abilities. There are many uncertainties in team sports that affect the final outcome and performance of the teams. These decisions range from team selection, tactics (e.g., choosing where players should be placed on a football field), player transfers (e.g., choosing which players should be sold to or bought from another team), and planning training sessions (e.g., to help players recover from injuries or improve collective performance of a team). The results of such decisions can sometimes be quickly obtained and learnt from (e.g., tactics may fail or succeed during a live game) or come through over a long period of time (e.g., a player may recover differently based on different long-term training regimes or preparatory matches).
In recent years, the field of team sports (teams, governing bodies, academies, etc.) has adopted a range of technologies that collect large amounts of data from training and matches that include the movement of players during games, their health statistics, and their actual performance during such games. Players train and compete while being monitored by a number of sensors to gain more information about performancesFootnote 2. This helps coaches and managers optimize training sessions and further improve performance. For example, companies such as OptaFootnote 3 and STATSFootnote 4 specialize in collecting and distributing sports data to teams and media outlets. Major teams around the world already use a variety of datasets to make decisions and improve their on-field performances. This tends to lead to increases in prize money, higher proportions of TV rights, and more sponsorship deals. For example, the promotion of an English Championship football team to the English Premier League (EPL) is worth £200 million in extra revenuesFootnote 5. Also, professional betting companies use such datasets to exploit inefficiencies in the sports betting markets and maximize their profits. Hedge funds who use the sports gambling markets as a way to make investments exploit these sports betting market inefficienciesFootnote 6.
Taken from a scientific point of view, the availability of such datasets presents a unique opportunity for the artificial intelligence (AI) and machine learning (ML) communities to develop, validate, and apply new techniques in the real world. Indeed, a number of works that attempt to solve real-world challenges (e.g., in disaster response Ramchurn et al. Reference Ramchurn, Wu, Fischer, Reece, Jiang, Roberts, Rodden and Jennings2015, Reference Ramchurn, Simpson, Fischer, Huynh, Ikuno, Reece, Jiang, Wu, Flann, Roberts, Moreau, Rodden and Jennings2016, and energy systems Vytelingum et al. Reference Vytelingum, Ramchurn, Voice, Rogers and Jennings2011; Alan et al. Reference Alan, Costanza, Ramchurn, Fischer, Rodden and Jennings2015) with AI techniques tend to rely on synthetic environments that ascribe standard probability distribution to the behaviours of the entities involved or the external phenomena that impact on their behaviours (e.g., simulating the spread of fires in disasters and the ability of fire brigades in extinguishing them, or the changes in energy consumption in power grids due to changes in energy pricing). In turn, in team sports, real-world data are available over long periods of time, about the same individuals and teams, in a variety of environmental contexts, thereby creating a unique live testbed for AI and ML techniques. Indeed, recent works such as Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) and Le et al. (Reference Le, Yue, Carr and Lucey2017b) have proposed and validated novel performance prediction and combinatorial optimization solutions that have advanced the multi-agent and ML state of the art. While research in AI for team sports has grown over the last 20 years, it is as yet unclear how they relate to each other or build upon each other as they tend to focus on either specific types of team sports or specific prediction and optimization problems that are but one part of the whole field. Hence, in this paper, we set out to survey the literature in AI for team sports and provide a structured framework within which existing and future approaches can be characterized and organized. By so doing, we aim to establish the current benchmarks, find common approaches across different types of sports, and provide the research community with novel computational challenges that have yet to be addressed or could provide real-world scenarios upon which existing AI and ML techniques could be validated.
In what follows, we elaborate on the four key areas that we have identified where decisions and predictions can be optimized due to the significant performance and financial benefits that they may have:
Match outcome prediction: Predicting the outcomes of sporting events is an important factor for a number of stakeholders. According to a BBC report, the global sports betting market is estimated to be worth around $244 billion with millions of bets placed all over the worldFootnote 7. This means that the prediction of match outcomes is key to the bookmakers who set the odds and the punters who place their bets. Match outcome prediction is also an important factor for teams that affects their tactical decisions and overall recruitment and game strategy during a season. There are many uncertainties that may affect the result of a given game and we will elaborate on these in the rest of this paper.
Strategic and tactical decision making: There are a number of key decisions in the team sports process that affect performance both in-game and behind the scenes. These decisions include player recruitment, tactics, team selection, developing youth players, and managing injuries. Player recruitment is one of the costliest parts of team sports due to the price of purchasing new players and the wages that they demand. The world’s highest transfer fee in football is £198 million for Neymar in 2017 and highest salary per season in the National Football League (NFL) is $76 million for Aaron Rodgers. The enormous values placed on these players are usually based on subjective measures by the clubs. This means that often large sums of money can be paid for a player who never lives up to the expectations of their price-tag (Dobson et al. Reference Dobson, Goddard and Dobson2001).
Fantasy sport games: Fantasy sports are games (onlineFootnote 8, Footnote 9, Footnote 10 or via newspapers) open to the general public where competitors are challenged to predict the performance of real-world sports teams and players, and to choose artificial or ‘fantasy’ teams composed of such players. The players in these fantasy teams are then awarded points based on their real-world statistics. It is estimated that over 50 million people play fantasy sports in the USA, while over 5 million people regularly play the Fantasy Premier League (FPL) in the UK alone. Fantasy sports presents a number of interesting computational challenges that can be addressed using AI methods. These challenges include but are not limited to prediction of individual player performance, forming optimal teams based on player performances, predicting the fluctuating player values, and creating betting strategies when entering fantasy teams into competitions.
Managing injuries: Injuries to professional players can have a huge impact on their careers. Injuries also cause the performance of a team to decline as well as costing teams large sums of money in wages to a player who cannot play. In an annual report by JLTFootnote 11, all the injuries in the EPL were assessed and it was shown that in the 2017–2018 season, £217 million in wages were paid to injured players. Due to this, teams in all professional sports are now investing significant efforts into predicting the risk of injury and helping prevent them. The predictability of injuries in sport is discussed in Lysens et al. (Reference Lysens, Steverlynck, van den Auweele, Lefevre, Renson, Claessens and Ostyn1984) which suggests that injuries may be an area where AI could help benefit teams and players due to the success observed when predicting health issues in the past (Srinivas et al. Reference Srinivas, Rani and Govrdhan2010).
In this review, we focus our attention on the six most popular team sports in the world: Association Football, Rugby Union, One-Day Cricket, American Football, Baseball, and Basketball. We explore the existing relevant literature, provide new insights based on our own analysis of key statistics, provide a number of frameworks to structure the computational challenges involved, and highlight open areas of research.
The rest of this review is organized as follows. Section 2 provides details of the team sports we focus on. Section 3 deals with the approaches that have been explored for predicting sporting match outcomes. Section 4 outlines the strategic and tactical decisions that are made in sports and AI solutions to aid these decisions. Section 5 focuses on fantasy sports games. Section 6 outlines how AI approaches are used to help predict and therefore prevent injuries in sport. Finally, Section 7 discusses the open research areas and how they can be approached and Section 8 concludes.
2 Background
In this section, we detail the key features of various team sports that present opportunities for AI research and impact. Table 1 shows the key aspects of the game that can be used for comparisonFootnote 12. In the sections that follow, we give a more detailed background of the six sports that we focus on and the different challenges that each of these presentsFootnote 13.
Table 1 Team sports features.

2.1 Association Football
In a game of Association Football, or football for short, each team aims to score goals (1 point) against the opposition (by getting the ball into a 24ft × 8ft goal) and the team with the most goals after the game duration wins. Football is the biggest sport in the world, making up 43% of the sports industry. There are hundreds of professional leagues across the world (e.g., the EPL and Spanish La Liga are two of the world’s most popular leagues). In a classic football league, each team plays every other team twice, once at home and once away. This means that the typical season consists of (2N) – 2 games, where N is the number of teams in the league (e.g., in the EPL there are 20 teams meaning each team plays 38 games). There are also a number of cup competitions that run alongside the main leagues (e.g., The Champions League and The FA Cup).
A number of factors can affect a game of football such as weather, the quality of pitch, and injuries. There are also a number of tactical decisions (e.g., team formation and style of play) that can increase a team’s chances of winning a game. The 11 players are set up in a formation with 1 goalkeeper and 10 outfield players. An example formation for the outfield players is 4-4-2 which commonly denotes 4 defenders, 4 midfielders, and 2 strikers. The team formation is a key decision in football tactics to which effects team performance. Teams can also make in-game player substitutions (up to 3 in a game) which can help change the team’s current in-game performance. Injuries happen across the football season, and this can have significant impact on the teams - in the 2016–2017 EPL season there were a total of 735 injuries, which are often preventable muscular injuriesFootnote 11.
Increasingly, player recruitment plays a big part in modern day football. Players are bought and sold between teams across the world. Youth players are developed through clubs academies until they are ready to play in the first team. They can also be loaned out to other clubs to gain more experience. What makes football different in comparison to the other sports in this paper is the rarity of goals. This is highlighted in Table 1 where Anderson and Sally (Reference Anderson and Sally2014) show that over the 2010/2011 season there is a goal scored on average every 69 minutes. Due to this, a draw/tie is much more common in football than in other sports.
2.2 American Football
In a game of American Football,Footnote 14 teams aim to score touchdowns while attacking (worth six points), which is followed by a kick (one point if scored). Teams can also score field goals (three points) or a safety (two points). A game-day squad is made up of 45 players split into the offence, defence, and specialFootnote 15 teams. The coach makes a decision on how these players are positioned when on the field of play and usually also makes decisions on what plays to run during the game (where a play is a tactic used to move the ball down the field). Many factors affect teams’ performances in American Football such as weather and even the air pressure of the ballFootnote 16.
American Football makes up an estimated 13% of the global sports market. However, it is mainly played in North America where the main professional league is the NFL. There are 32 teams that make up the NFL, each team plays 16 games in the regular season. The teams that do well in the regular season make it into the playoffs where teams play up to four more games to determine the winner of the league. In the NFL, players are traded rather than bought or sold as in football and, instead of having youth teams to develop younger players, players are drafted from the college leagues. Much of the team and player performances in American Football are easier to quantify than other sports in this paper. This is due to the nature of the game as the yards that teams gain (which lead to points being scored) or prevent are measured and attributed to each player that contributes.
2.3 Rugby Union
In Rugby Union, each team aims to score triesFootnote 17 against the opposition, these are worth five points and are followed by a conversion—a kick at between the posts, worth two points. Teams can also score points through penalties and drop-goalsFootnote 18, both worth three points. The team with the most points after 80 minutes wins. Teams are split into forwards and backs where the forwards are the eight players that make up the scrumFootnote 19. Unlike football, there is a standard way to set up players on a rugby field so there is not a formation decision for the coach to makeFootnote 20. There are still many other tactical decisions for the coach to make such as player selection, line-out formation, and style of play. Usually, club rugby is played in a league format similar to football where each team plays against every other teams both home and away [e.g., in the Aviva Premiership (England) there are 12 teams, each play 22 games in a season]. Rugby Union has been the fastest growing sport since it became professional in 1995. It is popular in countries such as Britain, Australia, New Zealand, and South Africa. Due to Rugby being a high impact sport, it presents many injury-related challenges. In particular, how can the medical teams be assisted and how can players be further monitored.
2.4 Basketball
In basketball, teams aim to score a point by getting the ball in the basket. When scored within a given zone, it is worth two points, outside of this zone it is worth three points. A free throw is worth one point. The winning team is the team who accumulate the most points. The main league is the National Basketball Association (NBA) in the USA, and it makes up about 6% of the global sports market. In the NBA, there are 30 teams, all teams play 82 games in the regular season and the top teams make the post-season playoffs (a knockout style competition to decide the overall NBA winner).
Basketball is the only team sport that we consider in this paper, which is played indoors at the professional level. Thus, weather-related factors do not have an affect on the game. Basketball is very high scoring in comparison to the others (as highlighted in Table 1). It is also much more fluid and faster flowing in comparison to the other American sports which similarly to football makes quantifying an individual’s impact on a game outcome more challenging. In the NBA, there are on average 296 passes per team per game, this compares to 453 per team per game in the EPL, although in football there are more players on the pitch over a bigger playing area. If we look at this per player, each basketball player makes 59 passes per game, whereas each football player completes on average 41 passes per game.
2.5 Cricket
Cricket is played in a number of forms (e.g., Test and Twenty20), in this paper we focus on One Day International games (ODIs) due to existing literature also being focused on ODI games. In an ODI, there is 1 innings per team made up of 50 overs each (1 over = 6 balls), which can end earlier if all batsmen are out. In each innings, the batting team aims to score runs and bowling team aims to take wickets and prevent runs being scored. The winning team is the team with the most runs scored in their innings. Cricket is hugely popular in countries such as India, England, and Australia. The Indian market in particular makes up the majority of the market and is reportedly worth $5.3 billion.
Hitting runs and taking wickets are the main metrics used to measure player performances. Cricket, like Baseball, relies on a number of individual performances by players which make up the team performance, whereas other sports rely more on the team performance as a whole. Due to both cricket and baseball being bat-and-ball games rather than invasion games like the rest of the sports in this paper means that they present different challenges and factors for us to consider. At the core of this is that, even though they are team games, the performance of players is mainly based on a 1v1 scenario (batsman vs. bowler). This means that when we evaluate or predict performance we can focus on how an individual batsman performs against an individual bowler or vice versa.
2.6 Baseball
Baseball is a game made up of nine innings, where an inning is made up of both teams batting (while the other team fields) until they receive three outs. The batting team aims to score runs (a batsman gets round all bases), the fielding team aims to strike batsman out (three swing and misses) and stop runs being scored. If the score remains tied at the end of the regulated number of innings, then an extra inning is played. The team with the most runs at the end of nine innings is the winning team. Baseball makes up 12% of the global sports market. The performances of the Baseball teams/players are often measured by key statistics based on their abilities to hit runs or get outsFootnote 21.
Baseball is mainly an American sport and the main league is Major League Baseball (MLB). In the MLB, there are 30 teams where every team plays 162 games in the regular season with the best teams making the playoffs. The playoff is a knockout-style competition formed of 12 teams, where each round is a ‘best out of 7 games’, to decide the ‘World Series’ winner. Teams play games much more frequently in a Baseball season than in other sports’ which may mean players have to be rotated more and monitored closely for injury.
3 Match outcome prediction
Prediction of sports match outcomes is a complex computational problem due to the range of uncertainties that can influence match results. These include, but not limited to the team configurations, the health of players, the location of the match (home or away), the weather, and team strategies.
Typically, match outcomes consist of up to three possible classes: home win, away win, and a draw/tie. The draw/tie is a more common result in football, but it is still possible in all the team sports we focus on. When predicting these outcomes, probabilities are assigned to each possible state that the game could end in. Some models also focus on predictions for the scoreline or spread. The scoreline is the number of points/goals scored by each team and the spread is the difference between the number of points scored by each team. These are typically more challenging to predict due to the increased number of possible outcomes. By assigning a probability to each possible scoreline in a match, we are able to solve the different prediction problems that are presented. Thus, the match outcome prediction problem can be defined as:
 \begin{equation} p(outcome) = \sum^M_{i=0} \sum^M_{j=0} p(X = i, Y = j)\end{equation}
\begin{equation} p(outcome) = \sum^M_{i=0} \sum^M_{j=0} p(X = i, Y = j)\end{equation}
 \begin{equation}outcome =\begin{cases}homewin \text{ if } X \gt Y,\\[3pt] awaywin \text{ if } X \lt Y,\\[3pt] draw \text{ if } X=Y\end{cases}\end{equation}
\begin{equation}outcome =\begin{cases}homewin \text{ if } X \gt Y,\\[3pt] awaywin \text{ if } X \lt Y,\\[3pt] draw \text{ if } X=Y\end{cases}\end{equation}
where X = home points/goals, Y = away points/goals, M = max possible points/goals.
The multiple sources of uncertainties that exist when predicting match outcomes are typically very difficult to characterize. In what follows, we highlight the accuracy of the bookmakers in team sports and elaborate on the approaches that have been applied to predict match outcomes, scorelines, and points spread. We explore the earlier literature that exists in statistics as well as literature outlining ML approaches.
3.1 Bookmakers accuracy
As we will show, some of the match outcomes problems, presented by the sports in this paper, are more predictable than others. Bookmakers use sophisticated pricing models that assign ‘odds’ to an outcome (which reflect the likelihood) to maximize their chances of making a profit, this is discussed in Graham and Stott (Reference Graham and Stott2008). By comparing who the bookmakers made favourite (shortest odds) and the actual match outcome, we calculate a percentage accuracyFootnote 22 and use this to evaluate how predictable each sports outcome is. This provides an estimation of the predictability of each sport. Bookmakers price markets based on their own predictions of the match as well as using the bets that are placed as an indicator of the likely match outcome.
To demonstrate the variability across team sports, we focus on the prediction of match outcomes (see Figure 1). As can be seen, football has the lowest accuracy showing it is the least predictable. This is to be expected due to the frequency of goals being far less than frequency of points scored in the other sports (as discussed in Section 2). A draw/tie is also much more common in football meaning there are three possible outcomes to consider instead of just two. Basketball is shown to have the highest accuracy by the bookmakers. This may be due to the high number of points scored in a game or a smaller playing area with less players.
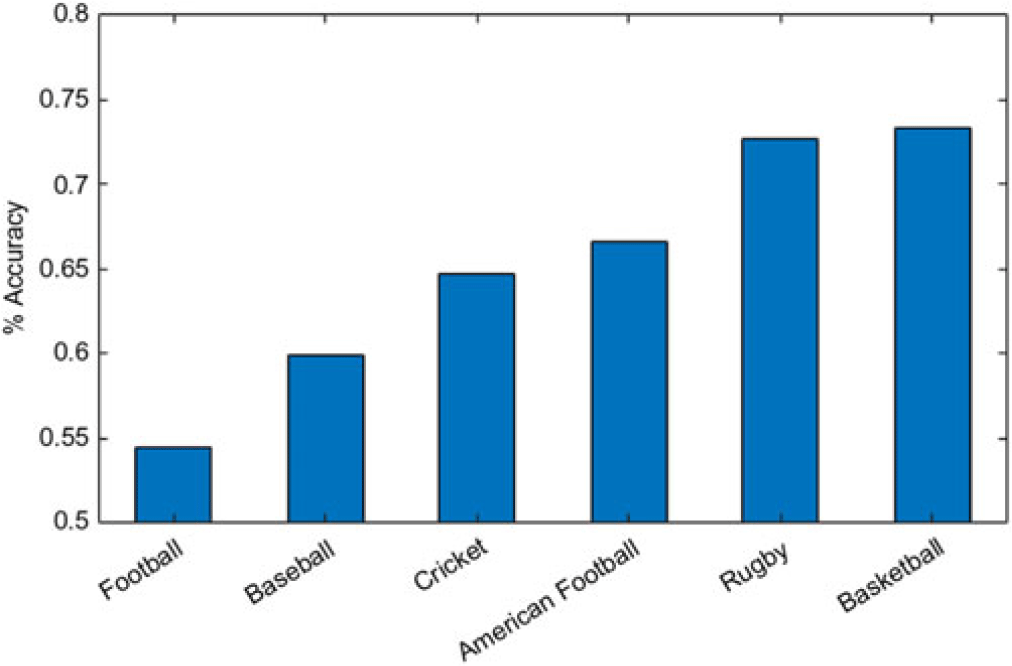
Figure 1. Bookmakers accuracy across 2017/2018 season
3.2 Statistical approaches
A number of studies have focused on finding ways that the game of football could be modelled and to find inefficiencies in the UK football betting market. Dixon and Coles (Reference Dixon and Coles1997) set out to exploit the inefficiencies and bias in UK football betting markets. Building upon the seminal work by Maher (Reference Maher1982), they developed an initial model to assign probabilities to each of the different game outcomes (home win, away win, and draw/tie). Using this, they are also able to form a new betting strategy. The model is based on the different abilities of both teams, calculated from prior matches. These abilities are broken into attack and defence and normalized based on the abilities of the opponents. Their model also takes into account a home advantage as discussed in Clarke and Norman (Reference Clarke and Norman1995). They are able to gain positive returns in a betting strategy. They use a technique based on a Poisson regression model, modifying Maher’s basic bivariate Poisson model to give Equation (3).
where λ = αi βj γ and μ = αj βi. In these equations, x and y represent the goals scored by the home and away team, respectively (![]() $[x,y] \in \mathbb{N}$
), α is the attacking parameter, β is the defensive parameter, γ represents the home advantage (
$[x,y] \in \mathbb{N}$
), α is the attacking parameter, β is the defensive parameter, γ represents the home advantage (![]() $[\beta,\gamma,\alpha] \in \mathbb{R}$
), and τ is a corrective factor used by Dixon and Coles to introduce an association between home and away goals that is missing in the independent Maher model. Finally, i represents the ID of the home team and j the ID of the away team. When the model described in Dixon and Coles (Reference Dixon and Coles1997) is run and tested across the past six seasons (2013–2019), it was found to have a prediction accuracy of 56.65%.
$[\beta,\gamma,\alpha] \in \mathbb{R}$
), and τ is a corrective factor used by Dixon and Coles to introduce an association between home and away goals that is missing in the independent Maher model. Finally, i represents the ID of the home team and j the ID of the away team. When the model described in Dixon and Coles (Reference Dixon and Coles1997) is run and tested across the past six seasons (2013–2019), it was found to have a prediction accuracy of 56.65%.
Dixon and Robinson (Reference Dixon and Robinson1998) studied the effect of the scoring rate which is changing depending on the current score of a game of football. They found that the scoring rate generally increases for both teams throughout the match, most likely due to tiredness of players that leads to mistakes in defending. They also found the scoring rates of home and away teams depend on the current score. Each scoreline is modelled as a different game state, and an example of the different possible game state changes throughout a game is shown in Figure 2.

Figure 2. Change in game state for a 3-3 scoreline (Dixon & Robinson Reference Dixon and Robinson1998)
When the scores are level, the scoring rates are similar to those at 0-0. If the home team is leading, the home and away rates generally decrease and increase, respectively. If the away team is leading, the rates of both home and away teams tend to increase. Their findings can be used to find match outcome probabilities and to attempt to improve on Dixon and Coles (Reference Dixon and Coles1997). This is done by finding the probability of each state (shown in Figure 2) and integrating over all the possible times and for each possible route to arrive at the final game state (x, y).
Crowder et al. (Reference Crowder, Dixon, Ledford and Robinson2002) again build upon the work of Dixon and Coles (Reference Dixon and Coles1997) by changing the original models’ calculations of attack and defence efficiencies. The new framework assumes that the efficiencies evolve through time (rather than remaining constant) according to some unobserved bivariate stochastic process. The original stochastic process model is replaced with an approximation that yielded a more tractable computation without comprising the predictive power. Dixon and Pope (Reference Dixon and Pope2004) evaluate the value and significance of the statistical forecasts from their earlier work in relation to betting market prices. They performed a detailed re-examination of match outcome odds and correct score odds across a number of years between 1993 and 1996. They suggest that the football betting market (at the time) remained inefficientFootnote 23 and the earlier models discussed in Dixon and Coles (Reference Dixon and Coles1997) could still be used effectively to earn positive returns when used with a strict trading rule to select the games to place a bet on.
More recently, Angelini and Angelis (Reference Angelini and De Angelis2017) were able to better the forecasting accuracy of Dixon and Coles. This paper uses a Poisson autoregression with exogenous covariates (PARX) model which is discussed in Agosto et al. (Reference Agosto, Cavaliere, Kristensen and Rahbek2016). By using this model, with the same betting strategy that is used in Dixon and Coles (Reference Dixon and Coles1997), they are able to generate betting return on investment of 33.62% on average when tested across three seasons (2013–2016 EPL). McHale and Scarf (Reference McHale and Scarf2011) focus on international matches instead of English League games. The authors present a new model for the number of goals scored by each team in a match and can be used for match outcome predictions. The model used in this paper is based on copula functions (Nelsen Reference Nelsen2006) which generate bivariate-dependent discrete distributions which are used to forecast the match scorelines. As this paper is based on international football matches, it may not be as successful if used for domestic leagues due to significant differences between international and league football. In comparison to the domestic leagues, there is a gulf in quality between teams that could play against each other internationally. Furthermore, international teams do not play as often. Therefore, datasets detailing the performance of international teams may not be as reflective of the current ability/form of the team and players. In a different study, Karlis and Ntzoufras (Reference Karlis and Ntzoufras2008) use the Skellam distribution (Skellam Reference Skellam1948) to predict the winning margin of games during the EPL 2006/2007 season. The Skellam distribution models the difference between two independent Poisson-distributed variables. Using these distributions, probabilities are assigned to the possible goal differences and therefore the match outcomes.
Turning to American football, there are a number of applications of statistical techniques to predict match outcomes and scoreline predictions. A birth-process model (Harville Reference Harville1980) uses a linear approach to create a baseline for NFL predictions in American Football, building on work that he had originally tested on college and high school American Football (Harville Reference Harville1976). More recently, Boulier and Stekler (Reference Boulier and Stekler2003) compare their model with human prediction and the bookmakers in the NFL between 1994 and 2000. They evaluate the use of ‘Power Scores’ (published in the New York Times) as a predictor by creating forecasts generated from probit regressors. A probit model is a type of regression where the dependent variable can take only two values, for example, home win or away win (Cappellari & Jenkins Reference Cappellari and Jenkins2003). This model was able to improve the accuracy of the predictions made by human experts. However, it was not able to improve the bookmakers’ accuracy. In turn, Leung (2014) uses the teams’ current ability based on other rating systems such as ‘Elo Ratings,’Footnote 24 which were initially designed to rank chess players (Coulom Reference Coulom2007). Leung makes predictions on the outcomes of college American Football matches using historic results and a sum of other metricsFootnote 25, the highest total sum is the predicted winner. The paper states that the model achieves a high accuracy, but it does not detail how this was tested. Finally, Baker and McHale (Reference Baker and McHale2013) look to predict the exact scores in a game of American Football. The authors use similar methods which were used for football in Dixon and Coles (Reference Dixon and Coles1997). The model takes each team’s attacking and defensive abilities and finds the probabilities of the final state of the game scoreline using a Chapman–Kolmogorov forward equation (Gardiner Reference Gardiner2009). This achieves an accuracy of 66.9% outperforming Boulier and Stekler (Reference Boulier and Stekler2003) who achieved 61%.
In basketball, Zak et al. (Reference Zak, Huang and Siegfried1979) calculate the production efficiency of points scoring for each team and using the ‘Richmond’ technique (Richmond Reference Richmond1974) they are able to estimate the potential scoring output of teams. Therefore, this could be used to make match outcome predictions. They also evaluate the basketball home-field advantage. Finally, ‘Yoopick’ (Goel et al. Reference Goel, Pennock, Reeves and Yu2008) outlines a different approach to create a sports prediction market. The market they create directly allows estimation of the entire point spread probability distribution within a single unified market. Punters bet on the outcome of the points difference of a game landing in a given interval with the interval prices determined by Hanson’s logarithmic market scoring rule market maker (Hanson Reference Hanson2007). This paper has yet to be tested against the accuracy of the more traditional betting markets.
In the next section, we will explore the ML methods that have been applied to the match outcome prediction problem for the sports this paper focuses on.
3.3 ML approaches
Most of the ML works involve Bayesian approaches and we focus on such approaches primarily. We also generally cover other approaches that have most recently come to the fore.
3.3.1 Bayesian methods
Bayesian methods have been particularly popular as they can be used to express hypotheses (potentially by experts in the game) and then learn the parameters that can lead to more accurate predictions. Another big strength of Bayesian methods is their ability to naturally quantify uncertainty, which is useful in sports where it is likely there are relatively few observations to draw conclusions from. Rue and Salavesen (Reference Rue and Salvesen2000) apply a dynamic Bayesian linear model to estimate the time-dependent skills of all teams in the EPL. These skills are used to predict the outcomes of the matches. The model uses a Markov-Chain Monte Carlo (MCMC) method to make estimations on the attack and defence abilities of teams. The MCMC method is particularly useful to model the change in abilities of the teams across the season; therefore, abilities need to be updated after each game-week. Previous results between teams are used to aid the predictions alongside the attack and defence abilities. They achieved an accuracy of 54%. At the time, this was slightly better than the bookmakers accuracy for the EPL and Division One results.
Joseph et al. (Reference Joseph, Fenton and Neil2006) compare a Bayesian approach to other ML approaches for predicting football outcomes. They test a number of algorithms on Tottenham Hotspur Football Club over the 1995–1997 seasons. The methods they compare are naive Bayesian network (BN), a data-driven BN (learns the structure of the network by using the correlation between the attributes), a K-nearest neighbour implementation, and a decision tree. The results confirm the potential of BNs when they are built by a reliable domain expert. The advantages of this model are able to provide accurate predictions without requiring large datasets. However, this work is focused solely on predicting the outcomes of a single team’s results which means it would have to be re-implemented for every team if used on a wider scale. Following on from this, Constantinou et al. (Reference Constantinou, Fenton and Neil2012) apply Bayesian models to football match outcomes across two Premier League seasons. Their model (known as pi-football) uses a number of variables such as team strength, team form, team psychology, and fatigue for both teams in a match to generate the outcome prediction. Some of their parameters are more subjective compared to team strength and form which can be calculated using the number of points a team has accumulated and goals scored/conceded. Pi-football is able to generate profits against maximum, mean, and common bookmakers’ odds. This model was improved further in Constantinou et al. (Reference Constantinou, Fenton and Neil2013) by identifying the key features (e.g., team strength, form, and fatigue with motivation) to reduce the inputs into the model. The number of features is reduced from 21 in total (10 for each team plus 1 representing discrepancy) to 10 (5 for each team). Other examples of Bayesian approaches to football match prediction include a study to predict results in the 2006 Germany World Cup (Suziki et al. Reference Suziki, Salasar, Leite and Louzada-Neto2009) and a Bayesian hierarchical model that was used to predict games in Italian football (Baio & Blangiardo Reference Baio and Blangiardo2008).
Moving away from football, Bayesian methods have been applied to other sports prediction problems. In American Football, Glickman and Stern (Reference Glickman and Stern1996) use a state-space model with Bayesian diagnostics to predict games in the NFL (tested on 1993 season). This paper focuses on predicting the points spread, as this is the main betting market in the NFL. They produce good results when compared against the ‘Las Vegas betting line’Footnote 26 but were unable to outperform it. Thus, their model achieves an accuracy of 58.2%, whereas the Las Vegas accuracy (at the time) was 63%. When comparing the mean-squared errors of the point differences, the model achieved 165.0 which was better than the Las Vegas result of 170.5. In Baseball, Yang and Swartz (Reference Yang and Swartz2004) use a two-stage Bayesian model to predict the winners of games in MLB. Data from the 2001 season and a MCMC algorithm are used to carry out Bayesian inference and to simulate outcomes of future games. This model performs well and can accurately predict the winning percentage of an MLB team across a season but it does not state the accuracy when used for individual match outcomes. Finally, there is an example of Bayesian models being used for cricket outcomes in Kaluarachchi and Aparna (Reference Kaluarachchi and Aparna2011). They test a number of methods to predict the winning team and their final model (known as CricAI) uses a naive Bayes classifier. On average, they achieved an accuracy of 0.593 when using the Naive Bayes approach.
The Bayesian methods that we have discussed in this section have produced some good results. However, they rely heavily on expert knowledge and also can be extremely intensive computationally for complex models. In the next section, we will explore other ML methods that have been applied to the match outcome problem and the results they achieved.
3.3.2 Other ML methods
A number of other ML methods have been applied to the sports match outcome prediction problem. In what follows, we elaborate on these methods and summarize their key properties in terms of outcome prediction.
Jayalath (Reference Jayalath2018) considers ODI Cricket prediction and focuses on quantifying the significance of important features using ‘classification and regression tree’ and logistic regression approaches. The study identifies that the key feature to improve a team’s chances of winning is home advantage. Building on this, Jayantha et al. (Reference Jayantha, Anthony, Abhilashab, Shaikb and Srinivasaa2018) create a model for predicting ODI games using ML techniques and also outline a team recommendation system, which is discussed in Section 4.3. The prediction model in the paper uses a support vector machine (SVM) model with linear, poly, and radial basis function (RBF) kernels. They use features such as batting and bowling averages to create power rankings for each player. The model takes the line-ups of the two teams and the player statistics in these line-ups. The SVM models are trained with historic win or lose percentages. When tested with the linear, poly, and RBF kernels, they achieve an accuracy of 70.83%, 68.75%, and 75%, respectively.
As discussed in Section 3.3.1, Joseph et al. (Reference Joseph, Fenton and Neil2006) apply other ML techniques beyond Bayesian approaches for football. A decision tree and a K-nearest neighbour model were developed. The MC4 decision tree achieved an overall average test percentage result of 41.72%. The K-nearest neighbour method uses a likeness approach, where the model finds similar instances to the test case and then a voting mechanism is used to predict the outcome. This performed better than the MC4 decision tree by achieving a test accuracy of 50.58%, the Bayesian approach in the same paper achieved an accuracy of 59.21%. Baboota and Kaur (Reference Baboota and Kaur2018) again looks at applying ML techniques to football match outcomes and compares the results to bookmakers. They use feature engineering and exploratory data analysis to find the feature set with the most important factors for predicting match outcome. They use a number of features with different weightings such as form, shots on target, goals, and more. They model the ternary classification problem to a binary classification one, and a prediction is made for whether a team will win the match or not. The methods that are tested by the authors are Gaussian naive Bayes, SVM (with RBF and linear kernels), random forest, and gradient boosting. They use training data from 2005 to 2014 in the EPL and they find that the best performing algorithm was the gradient boosting method (56.7%), followed by the random forest (56.4%), SVM models (RBF 54.5%, linear 54.2%), and then finally the poorest performing was the Gaussian naive Bayes method (52.6%). Similarly, Hucaljuk and Rakipovié (2011) test a number of features and classifiers. The features they use are the form of the team, previous meetings of the teams, current league position, number of injuries, and average number of goals scored and conceded in a game. Six different learning classifiers are tested using these features: Naive Bayes, Bayesian Networks, LogitBoost, K-nearest neighbours, random forest, and artificial neural networks. Datasets from the UEFA Champions LeagueFootnote 27 (a cup competition as mentioned in Section 2.1) are used in this paper, focusing on only 96 games. They achieve an accuracy of up to 68% when using neural networks. This is considerably higher than results in the EPL. This may be because in the Champions League, the best teams in Europe’s top leagues compete against weaker teams from smaller football nations in the earlier stages of the competition meaning the match outcomes are more predictable. There are also fewer games played in the Champions League, so there are less data available for testing the models as shown by the test-set in this paper only using 96 games.
McCabe (Reference McCabe2002) uses neural networks to predict games of Rugby LeagueFootnote 28 in Australia. This work is extended in McCabe and Trevathan (Reference McCabe and Trevathan2008) where again a model is created with a neural network system using a multi-layer perception with a number of different features such as prior performance data, game location, and team rankings. This model is able to perform well in Rugby League competitions with the average accuracy reaching up to 67.5%. This work was also applied to football results in the EPL. The results from this were compared to top human expert ‘tipsters’ who also make weekly predictions on the same games in the form of a competition called TopTipperFootnote 29 and they were able to reach the top percentile with the model against the other human experts.
Shi et al. (Reference Shi, Moorthy and Zimmermann2013) consider the problem of predicting college basketball games in the US NCAAB league. Five different ML models are developed: decision trees, rule learners, artificial neural networks (multi-layer perception), naive Bayes, and a random forest, using data from 2009 to 2013. The methods all achieve between 68.4% and 74.5% accuracy. Their evaluation shows that a high level of accuracy is achieved when using neural networks, and this can be used to beat humans predictors. Finally, part of the work performed in Landers and Duperrouzel (Reference Landers and Duperrouzel2018) focuses on making predictions on NFL match outcomes and point spreads which they apply to ‘Pick’em’ styleFootnote 30 online competitions. Their model uses 28 features such as bookmakers favourite, average points (home and away), game location, and more team performance-related statistics. These features are used with an average perceptron and a boosted decision tree classifier algorithm to create their model. They tested the model over three NFL seasons and find the decision tree provided the best results achieving an average accuracy of 58%. This work is compared to Boulier and Stekler (Reference Boulier and Stekler2003) (discussed in Section 3.2) which achieves 61% and to the bookmakers who achieve 65.8% accuracy.
In Table 2, we summarize the ML approaches that have been used for match outcome predictions. These algorithms mainly use key team performance metrics as their features such as points/goals scored and conceded, league position, and form. However, there are some key factors that are not yet accounted for by the approaches that we have discussed. These are largely the external factors that can impact the results of sports outcomes (e.g., weather, player moods, changes in coaching, player transfers, or impact of injuries).
Table 2 ML approach summary.

In this section, we have evaluated the different approaches that have been used to make sports outcome predictions. Across all the different forms of predictions that we have discussed, all appear to reach a ‘glass ceiling’ which we discuss further in Section 7. The papers we evaluated also show that football is the hardest game to predict due to the low-scoring nature of the game. There are many decisions that impact the outcome of sports matches. In the following section, we explore some of the decision-making processes that exist in team sports.
4 Strategic and tactical decision making
In this section, we turn our attention to the key decisions that arise when managing sports teams. In particular, to structure our discussion we propose a new framework (see Figure 3) which captures the key processes that operate in team sports and the interconnection among these processes that create a number of feedback loops. Using such a framework, it is then possible to understand the importance of both machine and human decision making throughout. In more detail, player transfers present a recruitment problem where teams want to ensure that they purchase the best possible players within their budgets. The squad of players then train to prepare for matches and develop their skills. During the training process, we can optimize the development of youth players to ensure they reach their maximum potential. The next stage focuses on decisions that are made to improve teams chances of winning games. This includes opposition analysis which supports the team selection and tactical decisions made by managers/coaches. Finally, these decision-making processes have feedback from the match outcomes and the in-game team performance.
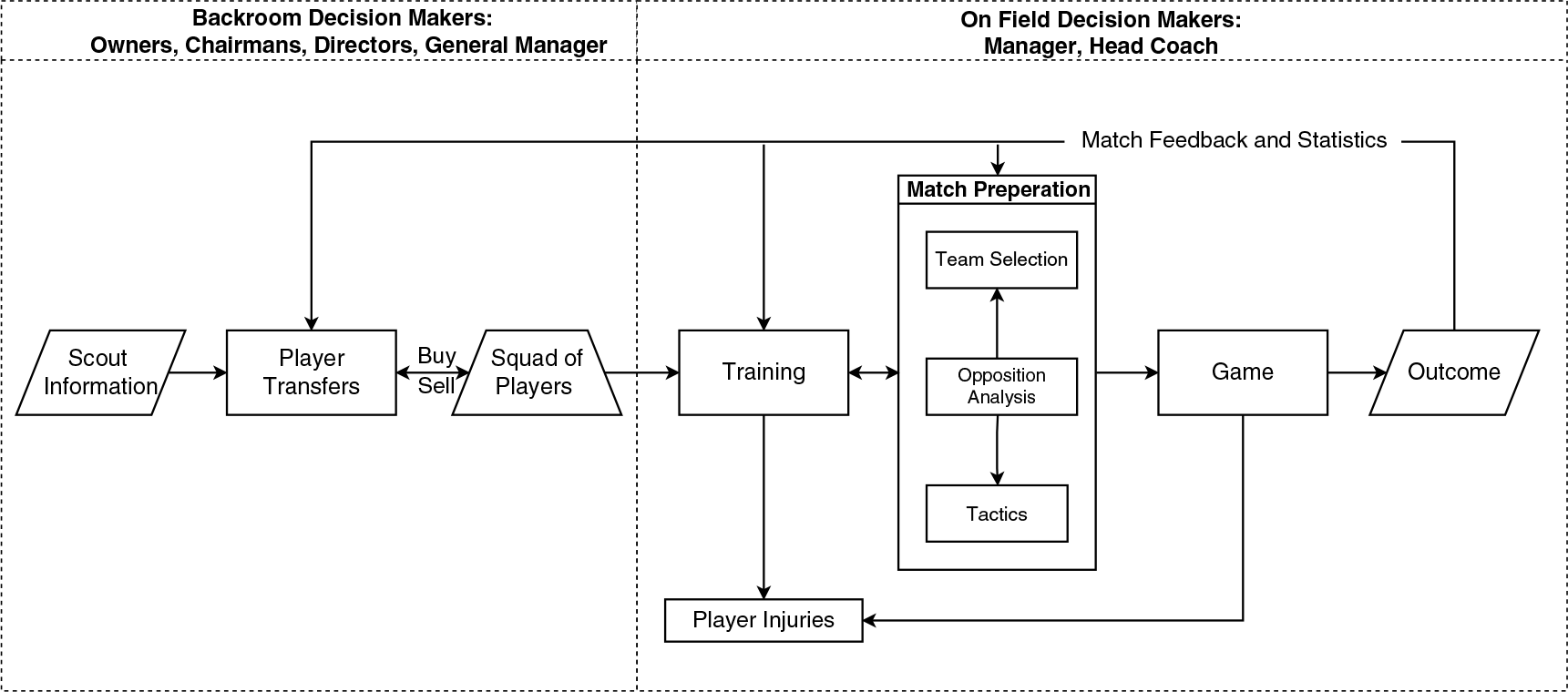
Figure 3. The team sports process
4.1 Player transfers
The recruitment of new players is a different process in every sport and usually involves decisions from managers/coaches alongside the directors higher up in the sports organizations. In football, players are bought and sold between clubs (as discussed in Section 2) whereas, in many American sports, players are draftedFootnote 31 and traded. In most cases, clubs gather information on players (scouting), therefore the amount teams pay for a player relates to how well they think that the player will perform in the future and how much they will impact the team. There are a number of elements that add uncertainty to the process, namely concerning whether a player will continue performing well, if the player will fit into their new team, if the player will settle in to a new environment/surroundings, and if the player will stay fit. These uncertainties are discussed when drafting a college player into the NFL in Hendricks et al. (Reference Hendricks, DeBrock and Koenker2003). Here, it is suggested that statistical discrimination and option value influence choices in this market meaning that some players could be over-valued. Modelling the uncertainties that exist in future performances of players and predicting how well they will impact a team would provide huge benefits to sports teams. This will allow the decision makers to evaluate the risk of player before paying large sums of money. These types of predictions can also help assign a monetary value to a player, so that a fair price is paid. There are a number of factors that affect the price of a player, some of these are explored in Dobson and Gerrard (Reference Dobson and Gerrard1999). In Figure 4, we show the generic recruitment process that sports teams follow when investing in new players.

Figure 4. The player recruitment process
All of the stages within the player recruitment process present different challenges that can be improved through the use of AI methods. These are discussed below and correspond to the numbered processes in Figure 4.
1. The first stage is identifying which areas in the team need to be improved. We can go about this firstly by looking at the statistics of the team performance to identify what in particular needs improvement (e.g., more goals in football or more wickets in cricket). We can also highlight which individual players are not pulling their weight in the team and look to improve these.
2. The next process is gathering intelligence on a large set of players, this can be done in a number of ways. Teams have access to league statistics where they can find information regarding player info. These statistics are becoming more detailed and could be used alongside AI to efficiently evaluate current ability and potential. This is an important inexpensive stage of the process as it can save money further down the line by avoiding sending scouts to watch players who are not right for a team. This can also help to identify players who are overlooked by other clubs and help find the best value players.
3. Once we have basic statistics on players, scouts are deployed who will gather more subjective information which may not be shown in the statistics. However, most teams have a limited number of scouts (N) and a limited scouting budget. Therefore, we must optimize this process so that the scouts time is not wasted and as many players are watched as possible.
4. The information that the scouts collect is collated alongside the statistics collected in process 2. Once all this information has been gathered, a team can use the statistics, scouts data, and scouts opinions to rank the players they have watched. Using this teams can identify the players they would like to sign to improve their team and estimate the costs involved for transfer fees and/or wages.
5. Usually in a transfer or trade window, teams will want to buy and sell multiple players to improve the squad. This presents a budget optimization challenge as we want to purchase as many highly rated players from the information gathering process who can positively impact the team. Therefore, the objective of this optimization is to maximize the quality of the players who are purchased while staying within the constraints of the transfer/wage budgets. There are also other constraints set by the leagues such as squad sizes and wage caps. Finally, if a team is to sell their current players, they can increase their transfer/wage budgets and create room for more new players. This is something that would need to be treated with caution though, as it could ruin the cohesion of the players within the team if we were to sell/buy too many players.
The processes we have discussed aim to improve the probability that a team will be successful in the transfer market and presents interesting computational challenges that are yet to be addressed by AI. The scouting process relates to AI literature which focuses on learning from imperfect classifiers. An example of this is shown in Simpson et al. (Reference Simpson, Roberts, Psorakis and Smith2013) where human decisions, with prior knowledge about the ability of that human’s decision making, are combined with Bayesian approaches to make decisions. This can be applied to scouting as we can use the teams scouts opinions on players, with the knowledge of their prior scouting performance, alongside AI methods to rate players. The challenge of deploying the scouts relates to optimization literature such as Dang et al. (Reference Dang, Dash, Rogers and Jennings2006), Ramchurn et al. (Reference Ramchurn, Polukarov, Farinelli, Jennings and Truong2010) as we aim to maximize the number of high quality players the scouts assess while meeting the time and budget constraints. The transfer budget optimization problem discussed in process 5 also relates to this literature as we are aiming to maximize the quality of players who are bought within the transfer and wage budgets where we can also sell current players to increase budgets.
Boon and Sierksma (Reference Boon and Sierksma2003) discuss the scouting of new team members to fill open positions and enhance the quality of teams. They calculate the potential value that new players into a team would have, focusing specifically on football. Their model uses linear programming to form an optimal team based on the quality of the players and their positional weightings that they calculate. Once an optimal team is formed they can use this for scouting purposes. Using a database of scouted players, players can be substituted into the team to calculate the effects that this would have and what value would be bought into the team. This model could be improved by taking into account the multiple positions that players can play in and the different roles players can take in different positions (e.g., a central midfielder could be a defensive player and sit deeper or could be more attacking to push further forward). Boon and Sierksma mainly focus on how scouted players will impact a team rather than looking to identify players who could be scouted and finding players who may have been overlooked by other teams. The challenges presented by player transfers could also be modelled as a case-based reasoning problem, where new players could be devised by evaluating similar players/transfers and similar situations that have happened in the past, by adapting the problem and solution to the new situation (Kolodner Reference Kolodner2014).
In the next section, we explore how teams train youth players in their academies which is another route that teams can take to improve their squad and bring in new players.
4.2 Training and developing players
Young players can be trained by professional teams from ages as young as sixFootnote 32. Thus, teams can play a huge part in how they develop players and how they bring these players into the first team squad once they are old/good enough. The process of bringing players through youth systems can be fine-tuned and optimized at many stages. This can involve making sure that their training is tuned to improve their skills efficiently and ensuring that they are given the right amount of experience at the right times either in the first teams or by being sent out on loan to smaller clubs. The challenge of personalizing the training regime of youth players therefore involves a number of prediction and optimization problems that could be addressed by AI techniques. This is particularly so when such training regimes need to cope with significant degrees of uncertainties in player performance (e.g., injuries, variability in mood, or weather conditions). A number of studies have explored the effects of injuries to youth players. Price et al. (Reference Price, Hawkins, Hulse and Hodson2004) highlight the nature and severity of injuries that occur at academy level, and le Gall et al. (Reference le Gall, Carling, Williams and Reilly2010) evaluate the fitness characteristics of young players in youth academies, highlighting which of these characteristics improve players chances of proceeding to higher levels.
De Silva et al. (Reference De Silva, Caine, Skinner, Dogan, Kondoz, Peter, Axtell, Birnie and Smith2018) have also used the player tracking data that are available as a tool for training youth players and for physical performance management in football. They tested their work in a professional Premier League football academy. This research uses standard statistical analysis to compare the activity demands in key playing positions, such as central midfielders and centre forwards. This study helps to provide insights from an elite performance environment regarding the relationship between player activity levels during training and matches and how they vary by playing position. This is an example of where ML-based analytics could be used by a top club to extend their knowledge and make changes to some of their training practices.
Finally, Fister et al. (Reference Fister, Ljubic, Suganthan, Perc and Fister2015) outline the challenges for computational intelligence in sport. The authors discuss the problems and current work that exist in sports (not just team sports) domain and in particular training for athletes. They open up a number of research questions in the area of training for sports and showed a necessity for developing an artificial personal trainer to optimize sessions. They also outline the process of sport training, showing the key components and a programming model. The paper mainly focuses on training which is not specific to any sport or skill such as for strength and power. However, it is still a useful tool for us to identify the stages in the team sport training process that can be optimized using AI.
Next, we turn our focus on the team selection problem where managers/coaches select the players to play in games.
4.3 Match preparation
Team selection is a key tactical decision in team sports which has to factor in a number of uncertainties. In essence, the challenge involves picking a set of players to play in a game, which will maximize the chances of winning. The selection must be from the registered squad of players as sports regulating bodies allow each team to select and register a squad of players governed primarily by financial criteria (e.g., in the EPL teams are allowed to register a squad of 25). Transfer windows give teams opportunities to make adjustments to their registered squad within the governing body’s rules.
There are many different combinations of possible team selections which is different for each sport. For example, in football, there is a squad of 25 players and need to select a team of 11; therefore, there are 4457400 different possible team line-ups. This is calculated using nCr where n is the number of players and r is the size of the team. It is worth noting that this would change depending on the formation of the team that is selected (number of defenders, midfielders, and forwards) as some players are unable to play in certain positions, in football there are a total of 165 possible formations that players could be formed in.
There are number of factors that coaches must consider when selecting a team. Examples of these include, but are not limited to: player injuries, players abilities to deliver the tactics/role, the opposition team, the current fitness of the players, and motivation of the coach to succeed in the game. The team selection process also involves thinking about developing younger players. This is a balancing act between selecting a team that will win against thinking about using youth players. In most cases, these players are bought into games as substitutes or are selected to be used in less important games such as pre-season friendlies or cup games. It is also important to note that we must consider how players will work together as a team with the other players who are selected.
In American football, cricket, and baseball, it is generally easier (compared to football and basketball) to identify which players have been performing well and therefore the challenge of finding a team that maximizes the chances of winning is slightly easier. That said, there is a lack of academic work which has focused on solving this problem. In football and basketball, it can typically be a challenge to attribute each player’s contribution to a team. In these sports, there are a number of other factors that make a good performance other than just scoring or creating goals.
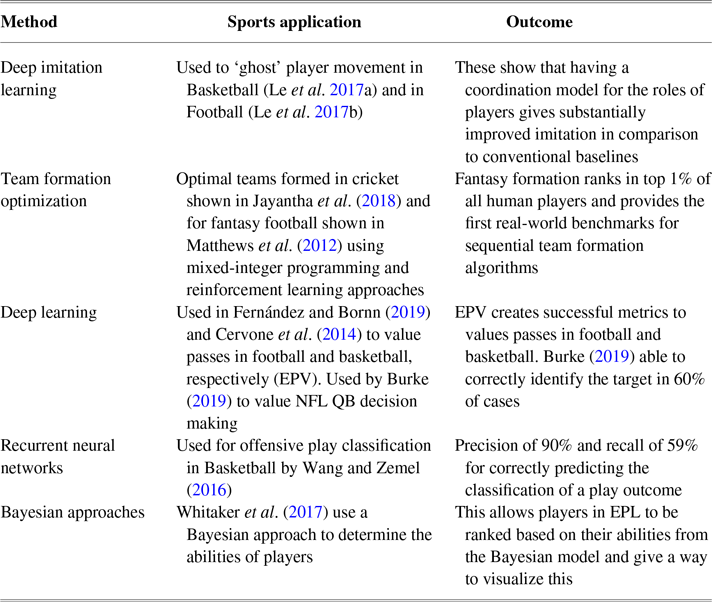
Deep learning has also been applied to model the behaviours of players in both basketball and football (Le et al. Reference Le, Carr, Yue and Lucey2017a; Seidl et al. Reference Seidl, Cherukumudi, Hartnett, Carr and Lucey2018). Here, deep imitation learning has been used to ‘ghost’ teams so that a team can compare the movements of its players to the league average or the top teams in the league. A simulation is run to see how an AI team would move in certain situations with the AI team created by ‘ghosting’ the characteristics of average and top teams. This helps to identify where teams can make changes to their players’ movements and change events to improve the probability of scoring a basket/goal or reduce the probability of conceding. Le et al. (Reference Le, Yue, Carr and Lucey2017b) are also an example of multi-agent approaches to imitate and learn the movements of players in a game of football. The authors show that having a coordination model for the roles of players gives substantially improved imitation in comparison to conventional baselines.
Other factors that may need to be considered in this area involve predicting what an opposition will do: their line-up, their formation, their set pieces, what style they will play, what areas of the pitch they target, where a player will aim a penalty, and many more. An example of work that forms teams based on an opposition is shown in Jayantha et al. (Reference Jayantha, Anthony, Abhilashab, Shaikb and Srinivasaa2018) where the authors create a team recommendation system for cricket teams which is based on selecting players who increase the probability of the team winning.
The team selection problem in sport relates to team formation literature in the multi-agents domain such as Chalkiadakis and Boutilier (Reference Chalkiadakis and Boutilier2012) which proposes new methods for coalition team formation. Coalition formation is the analysis of one or more groups of agents, called coalitions, that together jointly determine their actions. They integrate decision making during repeated coalition formation under type uncertainty using Bayesian reinforcement learning techniques. Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) form optimal teams for fantasy sports games under the constraints that the fantasy sports problem presents (discussed further in Section 5.2). They do this by predicting the performance of football players (in terms of how may fantasy points they will score) and then form a team which maximizes the number of expected points. This could be extended to aid team selection for sports teams and improve teams chances of winning. Vilar et al. (Reference Vilar, Araújo, Davids and Bar-Yam2013) discuss the complex social systems that are presented by team sports. The authors focus on the pattern-forming dynamics that emerge from collective offensive and defensive behaviours. They evaluate the differences in strategies and formations of two teams in a single game of football to understand the successful and unsuccessful relationships in the teams. This type of study provides significant results to demonstrate how complex systems analysis can help to better understand performance in football, by assessing team behaviour as a collective rather than individually. Forming optimal team line-ups in football is also discussed in Boon and Sierksma (Reference Boon and Sierksma2003) which we discussed in Section 4.1 where the form teams based on the players ability and how able they are to play in each position.
There have also been game theoretic approaches to optimizing teams of agents in other domains. These approaches have shown success in real-world applications. An example of this is shown for Stackelberg Security Games (SSGs), the success of SSG is discussed in Sinha et al. (Reference Sinha, Fang, An, Kiekintveld and Tambe2018). In an SSG, a defender must defend a set of targets using a number of resources, whereas the attacker is able to learn the defender’s strategy and attack after planning. Fang et al. (Reference Fang, Stone and Tambe2015) use game theory and the application of an SSG to optimize protection of endangered animals and fish stocks.
An important factor to be considered in the team selection process is to ensure that the players selected in the team are right for the team tactics. The approaches to tactical decision making, made by the manager/coach, are discussed in the next section.
4.4 In-game tactics
The in-game tactics used by teams to enhance their chances of winning games vary a lot from sport to sport. When creating tactics there are many factors that must be considered such as the opposition team and their weaknesses as well as the ability of the players available. Getting tactics right can give teams a huge advantage and can allow weaker teams to win games that they are not expected to. In football, tactics covers the formation that the team will use, the ‘style’ that they play in, set piece selection, and many more. In American Football, tactics cover the plays that are selected by the coaches and coordinators.
There have been a number of studies that aim to better understand the tactics in sports. One aim of these papers is to assess the impact of the individual actions performed by players during games. Decroos et al. (Reference Decroos, Bransen, Van Haaren and Davis2019) aim to do this by creating a framework to value any type of player action based on its impact on the outcome of a game and use a CatBoost (Prokhorenkova et al. Reference Prokhorenkova, Gusev, Vorobev, Dorogush and Gulin2018) approach to achieve this. Fernández and Bornn (Reference Fernández and Bornn2019) provide a model to assess the expected ball possession that each team should have in a game of football. The expected possession value (EPV) assigns a point value to every tactical option available to a player at each moment of a possession, allowing analysts to evaluate each decision that a player makes. In this paper, ML is used to estimate the parameters which are used in the model, such as pass and turnover probabilities which are estimated using logistic regression. A similar model is also applied to basketball (Cervone et al. Reference Cervone, D’Amour, Bornn and Goldsberry2014) where points are predicted and player decisions are valued. Similarly, Yue et al. (Reference Yue, Lucey, Carr, Bialkowski and Matthews2014) focus on play prediction in basketball developing models for anticipating near-future events given the current game state. These models are validated using 2012/2013 NBA data and show that their model can make accurate in-game predictions. Building on this, Zheng et al. (Reference Zheng, Yue and Hobbs2016) study the problem of modelling spatiotemporal trajectories of the players using expert demonstrations. In particular, they look to see how a basketball player makes decisions with long-term goals in mind, such as moving around opposition players or scoring points. They propose a model that uses both long-term and short-term goals and instantiate this as a hierarchical neural network trained using a large dataset of tracking data from professional basketball games. They show that this model generates more realistic trajectories compared to non-hierarchical baselines as judged by human expert sports analysts. This work could be improved by modelling the defensive team as well as the offensive team to give a more accurate simulation of the plays. Finally for basketball, Wang and Zemel (Reference Wang and Zemel2016) focus on offensive play call classification. This helps teams understand the opposition’s strategies to influence the final match outcome. They apply variants of neural networks to SportVUFootnote 33 tracking data and find they are able to label play sequences quickly with high precision. Using a recurrent neural network (RNN), they are able to achieve a precision of 90% and recall rate of 59% (when making predictions if the probability of the classifier is above 70%). There is a difficulty to annotate datasets in sports, especially when using spatiotemporal data due to a level of subjectivity. Active learning Cohn et al. (Reference Cohn, Ghahramani and Jordan1996) could be used for this, where the data labelling cost can be significantly reduced.
Other papers that focus on tactics in team sports include Bojinov & Bornn (Reference Bojinov and Bornn2016) which evaluates how in football a ‘pressing’ tactic affects performance and disrupts the opposition’s defences. By doing so, they are able to define and learn a spatial map of each team’s defensive weaknesses and strengths which is useful for coaches when preparing to face an opposition. In a similar fashion, Hobbs et al. (Reference Hobbs, Power, Sha, Ruiz and Lucey2018) aim to quantify the value of transitionsFootnote 34 in a game of football. They aim to explore how teams create goal-scoring opportunities based on their transitions and find that if a team counter-attacks immediately rather than looking to maintain possession, the chances of scoring rise by 4.4% and chances of having a shot rise by 24.4%Footnote 35.
Power et al. (Reference Power, Hobbs, Ruiz, Wei and Lucey2018) focus on set pieces in football (e.g., corners, free-kicks, and penalties). They discuss a number of ‘myths’ regarding set pieces and then prove/disprove these myths. For example, they show that a team is more likely to score from set piece than in normal possession (1.8% chance of scoring from set-pieces vs. 1.1% in open play). They also find that the type of delivery and the defensive set-up of the oppositions can significantly affect the chances of scoring. Finally, Lucey et al. (Reference Lucey, Bialkowski, Carr, Foote and Matthews2012) model team behaviours in football using entropy maps, created from teams ball movements, which give a measure of predictability of team behaviours across the field. This provides a useful tool for coaches and decision makers to be able to analyze opposition teams.
We have highlighted the studies that focus on the tactics within team sports. These approaches aim to decompose and break-down how teams play which give more interesting insights for coaches. This can be useful for teams when setting up their own tactics to maximize their chances of winning against another team. In the next section, we explore work that focuses on individual players’ performances.
4.5 In-Game player performance
Measuring player performance is an important factor in the decision-making processes in team sport. This helps to provide the feedback to identify when changes need to be made to team line-ups, tactics, and when transfers need to be made. A number of papers focus on ways to measure performance objectively with data. Whitaker et al. (Reference Whitaker, Silva and Edwards2017) use a Bayesian approach to determine the abilities of players using a number of different event types. They implement a Poisson model for event types and can then infer player abilities from this. These inferences allow EPL players to be ranked and differences between players to be visualized. Power et al. (Reference Power, Ruiz, Wei and Lucey2016) focus on measuring the risk and reward of passes in a game of football. This gives new methods to evaluate player passing performance and identify key players in a team who execute the key passes consistently. Similarly, McHale and Relton (Reference McHale and Relton2018) also aim to identify key players in a team by using network analysis and pass difficulty in a game of football. They aim to provide analysis to managers and coaches for them to identify their best team line-up, and in the analysis of opposition teams.
Power et al. (Reference Power, Cherukumudi, Ganguly, Wei, Sha, Hobbs, Ruiz and Lucey2019) focus on the performance of football goalkeepers. They simulate each goalkeepers performance when facing a number of example shots and compare which goalkeeper would concede the least number of goals. They do this by using a ‘spatial descriptor’ for each goalkeeper which is made up from features such as clean sheet percentage, win percentage, and save percentage for different thirds of the goal. This type of player performance modelling was also explored within baseball to evaluate how a batter will perform against certain pitchers (Alcorn Reference Alcorn2018). In these papers, players’ performances are simulated in different scenarios to give a basis for a fair comparison of players. This type of analysis could be built on in all sports to identify the impacts that the individuals have within the complex team systems. Coaches could use this to identify how changes in their style of play, with their current set of players, would affect the performance of the team. Theses simulations could also be used for player recruitment as potential new players could be simulated to show how they would perform in a new team.
Turning to basketball, Felsen and Lucey (Reference Felsen and Lucey2017) evaluate NBA players’ body pose and shooting styles to find any correlations between the player body shape and shooting success. They find statistically significant differences in distributions of attributes describing the style of movement of different phases of the shot. In American Football, Burke (Reference Burke2019) uses deep learning to quantify quarterback (QB) decision-making again allowing us to identify the NFL QB’s who have the best decision-making skills, this is a vital part of the QB position in a game of American Football. Their model correctly identifies the targeted receiver in 60% of cross-validated cases. They find when passers target the predicted receiver, passes are completed 74% of the time, compared to 55% when the QB targets any other receiver. Their approach gives a new way for teams to quantitatively assess QB decision-making performance. Finally, Correia et al. (Reference Correia, Araujo, Craig and Passos2011) assess players’ decisions when making passes in Rugby Union based on the positions of oppositions and team mates.
In Table 3, we summarize the AI approaches that have been used for sports strategies and decision making.
Table 3 Strategy and decision-making AI approach summary.
The majority of the work that we have discussed in this section focuses on finding new insights into tactical analysis in sport. These studies help identify the strengths of different tactical process and find new ways of evaluating player and team performances. There are good examples of work in football and basketball however not as many in American football or rugby where tactical decisions are also key to winning games. There still remains a number of areas where AI could impact tactical decision making. This work would mainly be focused around how individual agents (the players) perform in different teams, with different tactics and how much impact they have on the game outcomes. This type of analysis could benefit all of the processes that we showed in Figure 3 as AI could improve player transfers, match preparation and help to gain better feedback from the outcomes of games.
In the next section, we turn our focus on fantasy sports games and the computational challenges that these present.
5 Fantasy sports games
As discussed in the Introduction, in America alone an estimated 32 million people take part in fantasy NFL games (American Football) with an average spend of $467 per person, per season totalling to around $15 billion across the season, and in the UK over 5 million people take part in the FPL for footballFootnote 36. There are fantasy sports games for nearly every professional team sport and there are many different sites and leagues ranging from competitions with millions of competitors to small leagues run between friends.
In fantasy sports, games competitors select a team of real-life players, who are assigned a value/salary, within a given budget. Depending on how well the players perform in real life they are given corresponding fantasy points (e.g., for a goal/assist in football or a touchdown in American football). The aim of the game is to maximize how many points the selected team can obtain under the constraints of the fantasy game. Figure 5 shows the process of fantasy sports games. Initial values, based on knowledge of the players ability, are set for the players before the season starts and the fantasy competitors select an initial team. This team of players is then awarded points each game-week based on their real-world performance (if the player does not play they receive no points). The values of the players can also be updated throughout the season so that the players who have performed better than expected will then cost the reflective amount. The fantasy league standings are updated each week and once all the N game-weeks have been completed, prizes are awarded based on the standings.

Figure 5. The fantasy sports game process
Traditionally people compete in a league across the season, with the aim to accumulate the most points while having restrictions on the number of changes/transfers that can be made to a team. In these games, the ‘game-week’ processes shown in Figure 5 are repeated for every set of matches (usually once a week). Leagues such as these have been running for many years. A good example of this is the FPL for football in the EPL, which is extremely popular in the UK and worldwideFootnote 37. In the FPL, there are 38 game-weeks therefore N = 38. This means that in fantasy games such as this the transfer stage is key to success as, depending on the fantasy league, the number of transfers are limited (e.g., in the FPL there is a limit of one transfer per game-week). Due to the rules on transfers, when selecting the initial team and making changes it is important to consider the players future performances as well as just the next game-week.
More recently, Daily Fantasy Sports (DFS) sites, such as FanDuelFootnote 9 and DraftKingsFootnote 8, have seen a large growth in popularity. These sites offer leagues that only run for one game-week rather than across the whole season, meaning that a new team is selected each week instead of making transfers. In these type of fantasy games, new teams are formed every week from scratch; therefore, in Figure 5, the value is N = 1. This means that only an initial team is set and only one future game needs to be considered when predicting the players’ performance.
Although there has been significant growth in fantasy sports, there is a lack of research focus into ways that AI could be used to improve competitors performances or using AI automated teams to compete against humans. There are a small number of studies in fantasy sports. The seminal work of this area is Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) provided the first real-world benchmark for sequentially optimal team formation in this domain. More recently, Landers and Duperrouzel (Reference Landers and Duperrouzel2018) use ML techniques for NFL fantasy leagues. When forming teams to enter into fantasy sports leagues, two key computational challenges are presented. These are:
• Player Performance Prediction: Predicting how well a player will perform in the real-world and therefore the number of points that a player will obtain both in a single game and over a given time period.
• Team Formation Optimization: Selecting an optimal team using the performance predictions so that the constraints of the fantasy league are met. This also includes the challenge of making effective transfers in the longer running fantasy leagues.
Both of these challenges can also be extrapolated to the challenges that exist in the real-world sport. As we have discussed in Section 4, it can be key to predict the performance of players in a team and then form optimal teams based on player predictions. As well as using AI to form teams and aid competitors fantasy performances, there are other challenges highlighted in Figure 5 that can be addressed using AI. Examples of these challenges are player price forecasts, opponent modelling after every match (as competitors are able to see other competitors teams), draft strategies and betting strategies to maximize the chances of winning cash in DFS fantasy games.
5.1 Player performance prediction
Predicting the player performance is key to selecting which players are worth having in a fantasy team. If a player (and the team he plays for) performs well, more points will be accumulated for the fantasy team. There are a number of factors that need to be considered when predicting how well an individual is likely to perform and this varies significantly based on the sport being played and the position that the player plays in. For example, in football when a striker’s performance is predicted, the aim is to predict the number of goals that he/she may score whereas for a defender we focus on predicting if his/her team will keep a clean sheet (concede no goals). Also, it must be considered how likely a player is to play in a given game, as players may not play due to injuries and tactical decisions. If a player does not play, they receive no fantasy points. These examples show a small number of many uncertainties that need to be considered when making predictions on future performances. The predictions of games (discussed in Section 3) can also be used to help predict the number of points that a player will score, as if a player is playing in a team which is likely to win then that player would have a better chance of scoring more fantasy points.
When predicting player points, a feature set for each player (in a given game week) is taken as an input, this is referred to as X where n is the number of features (shown in Equation (4)). Example features for an American Football player would be yards gained per game, number of touchdowns scored, and games played. In football, example features would be goals scored, number of assists, number of clean sheets, and minutes played. The feature set could also be made up of previous fantasy points scored from a number of prior weeks. Once a feature set is formed, a target vector Y represents the points scored by the player in the given game week, corresponding to the feature data in X. Equation (4) shows X and Y for n features and i players where p ix n is the n feature for the i player and p iy w is the ith player’s points in game-week w. Next, a ML algorithm can be trained using X and Y to produce a function φ that can output the prediction of Y using the features in X. A row of X, X j can be used with this to make a prediction on the corresponding row in Y. This gives φ(X j) = Y j. Different ML methods can be tested across the different sports.
 $$X = \left( {\matrix{
{{p_1}{x_1}} & {\quad {p_1}{x_2}} & {\quad {p_1}{x_3}} & {\quad {\rm{ }} \cdots } & {\quad {p_1}{x_n}} \cr
{{p_2}{x_1}} & {\quad {p_2}{x_2}} & {\quad {p_2}{x_3}} & {\quad {\rm{ }} \cdots } & {\quad {p_2}{x_n}} \cr
\vdots & {\quad \vdots } & {\quad \vdots } & {} & {\quad \vdots } \cr
{{p_i}{x_1}} & {\quad {p_i}{x_2}} & {\quad {p_i}{x_3}} & {\quad {\rm{ }} \cdots } & {\quad {p_i}{x_n}} \cr
} } \right)Y = \left( {\matrix{
{{p_1}{y_w}} \cr
{{p_2}{y_w}} \cr
\vdots \cr
{{p_i}{y_w}} \cr
} } \right)$$
$$X = \left( {\matrix{
{{p_1}{x_1}} & {\quad {p_1}{x_2}} & {\quad {p_1}{x_3}} & {\quad {\rm{ }} \cdots } & {\quad {p_1}{x_n}} \cr
{{p_2}{x_1}} & {\quad {p_2}{x_2}} & {\quad {p_2}{x_3}} & {\quad {\rm{ }} \cdots } & {\quad {p_2}{x_n}} \cr
\vdots & {\quad \vdots } & {\quad \vdots } & {} & {\quad \vdots } \cr
{{p_i}{x_1}} & {\quad {p_i}{x_2}} & {\quad {p_i}{x_3}} & {\quad {\rm{ }} \cdots } & {\quad {p_i}{x_n}} \cr
} } \right)Y = \left( {\matrix{
{{p_1}{y_w}} \cr
{{p_2}{y_w}} \cr
\vdots \cr
{{p_i}{y_w}} \cr
} } \right)$$
When making player performance predictions in a daily fantasy contest, we can be much more precise as the predictions only need to focus on how that player will perform in the specific game. Whereas, in more traditional leagues, future performances must be considered as well as just the next game. Thus, a player who will perform well in multiple future games will be selected and not just one who will perform well in a single game (which may be against a poor opposition). This is considered by the model shown in Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) where predictions for a players’ performance are made for a number of future game-weeks.
Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) predict a player’s performance and the number of points that a player will score based on the prediction of a given game using the Dixon & Robinson (Reference Dixon and Robinson1998) framework. The authors choose to use this approach as the Dixon and Robinson model treats football as a dynamic situation-dependent-process as well as its proven success in the football betting domain. Dixon and Robinson’s score predictions work by taking each club’s attacking and defending efficiencies from past results and then using these to derive the probabilities of the side scoring a goal in a given match (discussed in more detail in Section 3.2). Using the match outcome prediction, Matthews attributes the probability of a player scoring points based on the four most significant point-scoring categories in the FPL.
1. Player appearance in a game (worth two points per player playing over 60 minutes and one point for any player playing under 60 minutes). For this, a three-state categorical distribution is used, the states are starting, substitute, or unused. Three probabilities are computed for each category and the highest probability is assigned to the player to obtain the predicted points.
2. Clean sheetFootnote 38 (worth four points to a defender/goalkeeper and one point to a midfielder). For clean sheets, the probability of a team not conceding can be calculated using the scoreline distributions from the Dixon and Robinson model and points can be predicted based on these probabilities.
3. Goals scored (worth six points for a defender/goalkeeper, five points for a midfielders, and four points for a striker). This is calculated using a Bernoulli distribution (Gelman et al. Reference Gelman, Carlin, Stern, Dunson, Vehtari and Rubin2004) or a Binomial distribution over a single trial, describing a players probability of scoring the goal given he was playing at that time.
4. Goals created (worth three points per player). Another Bernoulli distribution is used for this, again describing the players probability of creating the goal given he was playing at the time.
Turning to American Football, the NFL study (Landers and Duperrouzel, Reference Landers and Duperrouzel2018) for player point prediction starts by engineering features from FanDuel that their model uses. In their paper, they test two different feature sets (FD 1 and FD 2). They also test two different methods and compare using the different feature sets. The methods they test are a least squares with averaged perceptron (Lehtokangas et al. Reference Lehtokangas, Saarinen, Kaski and Huuhtanen1995) and a boosted decision tree (Schapire Reference Schapire2003). These methods are evaluated using the coefficient of determination (R 2) to measure the accuracies (R 2). The boosted decision tree achieves average accuracy of 0.417 using FD 1 and 0.250 using FD 2 while the least squares approach achieves 0.401 on FD 1 and 0.146 on FD 2. Other related work has shown similar results to those in Sugar and Swenson (Reference Sugar and Swenson2015). It is noted that different methods could be tested for different positions in American Football. This is because the roles of different positions differ more than in other sports (e.g., QB vs. running back).
The current studies for player predictions show applications of ML techniques providing good benchmarks in both football and American Football. Further techniques could be tested in these sports to improve the current benchmarks. These could also be tested with new feature sets such as time-series data which would analyze the form of the players over a given number of game-weeks. Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) focus on the FPL fantasy game, it may be useful to test this work on a DFS site to see if it also performs well in these fantasy games. Landers and Duperrouzel (Reference Landers and Duperrouzel2018) only focus on DFS so it would also be interesting to see how their predictions would work in a more traditional multiple-week league. There also remain gaps in the literature for predicting performances of players in other sports where fantasy games are popular such as Basketball and Baseball.
The player score predictions become more valuable when combined with a good team optimizer, allowing the maximum points to be accumulated each week. The methods for team formation that currently exist in the literature are outlined in the next section.
5.2 Team formation optimization
Selecting the best team of players within the given constraints of the fantasy site is vitally important, and as shown in Figure 5 this process is repeated sequentially across a season with constraints for changes that can be made to the team. This process involves choosing players with different abilities, prices, and risks that need to be considered. As discussed in the previous section, we may also need to consider the future performances of these players over a number of given game-weeks. In formation problems, there are a number of actors, with their own abilities and characteristics that have form a team to perform a task to achieve a common objective in a real-world domain. Within the fantasy sports team formation problem, there are a number of players (the actors) with their own abilities (predicted points) and we are looking to maximize the number of these points (the common objective). Therefore, it is key to get the best players possible into a high performing fantasy team. The fantasy problem relates to other works in the AI community. In particular, Dang et al. (Reference Dang, Dash, Rogers and Jennings2006) focus on choosing the best sensors to survey an area, Ramchurn et al. (Reference Ramchurn, Polukarov, Farinelli, Jennings and Truong2010) focus on dispatching optimal teams of emergency responders, and Chalkiadakis and Boutilier (Reference Chalkiadakis and Boutilier2012) look at the appropriate set of agents to work within a coalition formation problem.
In fantasy sports, the main aim is to select a number of players, all of whom are assigned a value, in different positions within a given budget. For example, in the FPL, there are around 500 players available to select from, all with a position and a given value and 15 need to be selected (2 goalkeepers, 5 defenders, 5 midfielders, 3 forwards). The total value of the selected team mostly not exceeds £100 m. Eleven of those fifteen players are put up as your ‘starting 11’ (in a selected formation) and they will be the ones who will earn your fantasy points. The remaining players are ‘subs’ and will automatically come into the starting 11 if one of the current players does not play. This means that the players are selectable in over 6.5 × 109 ways. One team is selected at the start of the season and then one transfer is permitted per game-week. In DFS competitions, a fresh team is created each week, therefore the optimization is simpler. Figure 6 shows example of team formation set-ups from FPL and DraftKings.

Figure 6. Example fantasy team set-ups. (a) FPL team selection. (b) DraftKings team selection
Formally, a generic fantasy sport team optimization problem can be defined as the following set of equations (excluding other different constraints that the different leagues have in place).
 \begin{equation}\left( \begin{array}{ccccc}p_1 \rightarrow pos_1 & \quad p_2 \rightarrow pos_2 & \quad p_3 \rightarrow pos_3 \\[3pt]
p_4 \rightarrow pos_4 & \quad p_5 \rightarrow pos_5 & \quad p_6 \rightarrow pos_6 \\[3pt]
p_7 \rightarrow pos_7 & \quad \dots & \quad p_n \rightarrow pos_i \\\end{array} \right)\end{equation}
\begin{equation}\left( \begin{array}{ccccc}p_1 \rightarrow pos_1 & \quad p_2 \rightarrow pos_2 & \quad p_3 \rightarrow pos_3 \\[3pt]
p_4 \rightarrow pos_4 & \quad p_5 \rightarrow pos_5 & \quad p_6 \rightarrow pos_6 \\[3pt]
p_7 \rightarrow pos_7 & \quad \dots & \quad p_n \rightarrow pos_i \\\end{array} \right)\end{equation}
where a player p is added to each of the i positions in the fantasy team (only if the players position matches the slot in the fantasy team, for example, a QB cannot be selected as the running back in the fantasy team).
 \begin{gather}
argmax\left(\sum_{n=1}^{N} {points}_{n}\right) \nonumber\\
\text{s.t. } \sum_{n=1}^{N}{selected_n} = teamSize \\
\sum_{n=1}^{N} {value}_{n} \leq budget\nonumber\end{gather}
\begin{gather}
argmax\left(\sum_{n=1}^{N} {points}_{n}\right) \nonumber\\
\text{s.t. } \sum_{n=1}^{N}{selected_n} = teamSize \\
\sum_{n=1}^{N} {value}_{n} \leq budget\nonumber\end{gather}
where n represents the ID of a player, which is used to identify if that player is selected (selected n = {0,1}) and what the player value is ![]() $ (value_n = \{\mathbb{Z}\}) $
. Our objective is to maximize the total number of points (
$ (value_n = \{\mathbb{Z}\}) $
. Our objective is to maximize the total number of points (![]() $ (points_n=\{\mathbb{R}\}) $
) while staying within the given team size and ensuring that the combined salaries/values of the players are below the given budget constraint.
$ (points_n=\{\mathbb{R}\}) $
) while staying within the given team size and ensuring that the combined salaries/values of the players are below the given budget constraint.
Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) approach the FPL team optimization as a sequential team formation problem which is formalized as a Markov decision process (MDP). The model in this paper considers the limited transfers that could be made meaning that the future performances of players are considered when making changes. A reinforcement learning approach is used, working under uncertainty regarding the underlying MDP dynamics. In an MDP, the agent (in this case the fantasy competitor) and the environment (fantasy game) interact continually, the agent selecting actions (by selecting a team each game-week) and the environment responding to these actions (in the form of points) and presenting new situations to the agent. Using an MDP means that the model is able to assess the possible rewards that come from the possible actions that are made (in FPL this would be the action of making a transfer). The problem can then be treated as an optimization problem. Matthews et al., set up the problem as a multi-dimensional knapsack packing (MKP) (Korte & Vygen Reference Korte and Vygen2012) and solve the optimization using IBM ILOG’s CPLEX 12.3. A number of different set-ups of the MKP were tested. These include Q-Learning and Bayesian Q-Learning with different parameters. By doing this, Matthews was able to obtain a model that ranked in the 1.1st percentile and gives a benchmark for how AI and ML models are able to perform in the FPL.
When forming fantasy teams for the NFL in DFS competitions, Landers and Duperrouzel (Reference Landers and Duperrouzel2018) compare four different approaches for team optimization, these are:
1. Selecting a completely random team to loosely model the behaviour of a human with no knowledge of the sport.
2. Selecting a random team from a filtered dataset with just the higher performing players. This is to loosely mimic the behaviour of a player with general knowledge about the sport.
3. A filtered optimized approach picks a team from the filtered set and uses a brute force algorithm to select the best team based on maximizing the predicted points that fits the constraints.
4. Filtered actual best selects the best possible team from the filtered dataset to give a view of what the best performing team would be (this approach does not consider the budget constraint on total player values).
Using the player points prediction models discussed in the last section, 100 teams are selected using each of the above methods for each prediction method. The authors are able to evaluate the performances using the following metrics: The average points return of the 100 teams, the maximum points return, and the percentage of teams that produce a profitFootnote 39. This is compared against the work in Sugar and Swenson (Reference Sugar and Swenson2015) which achieves a success rateFootnote 40 of 71.4%, whereas Landers and Duperrouzel (Reference Landers and Duperrouzel2018) achieve a success rate of 82% for weeks 3–9 in the 2016 season. However, this would need more testing due to the small sample size (seven game-weeks) meaning the results are not statistically significant.
Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012) were able to achieve good results by solving their optimization problem as an MKP. As a brute force method for team optimization is used on a filtered dataset in (Landers and Duperrouzel, Reference Landers and Duperrouzel2018) there may be more efficient ways for this to be done, such as a similar approach using CPLEX in Matthews et al. (Reference Matthews, Ramchurn and Chalkiadakis2012). Using this type of approach would ensure an optimal team is selected and improves the run-time efficiency in comparison to a brute force approach. Another area to explore would be to model the uncertainties in the players’ performances rather than predicting their points. This would allow teams with different levels of risk and reward to be selected which may be useful in a DFS competition as multiple teams can be entered. This could be achieved by using a stochastic optimization approach (Ermoliev & Wets Reference Ermoliev and Wets1988). There also remain gaps in the fantasy sports process where AI could be used to forecast the player prices, assess opponents fantasy teams, and create AI betting strategies to maximize the chances of generating profits in DFS fantasy games. DFS strategies are discussed in Haugh and Singal (Reference Haugh and Singal2018) where a portfolio of teams is used to maximize the chances of generating profits.
In Table 4, we summarize the approaches that have been used for the points prediction and optimization in the discussed papers. In the next section, we will discuss the impact that injuries have to sports teams and how AI can be used effectively in this domain.
Table 4 Fantasy sports approach summary.

6 Injury prediction and prevention
Contact team sports have a high risk of injury (Drawer & Fuller Reference Drawer and Fuller2002a). If a team is missing their star players, the probability of winning matches decreases significantly. Moreover, it is not financially beneficial to pay large wages to players who are unable to play. The economic impact of injuries is highlighted in the annual report by JLTFootnote 11 who evaluate the injuries that occur in the Premier League every season. They found in the 2016–2017 season over £175 million of wages were paid to injured players. The impact in football is also discussed in Drawer and Fuller (Reference Drawer and Fuller2002b). Being able to predict when these injuries are likely to occur and change real-world variables to reduce the likelihood of the injury presents an interesting computational problem. Lysens et al. (2012) discuss the predictability of sporting injuries.
Vast amount of data is now collected in relation to individual players in both competitive matches and training. All professional sports are now collecting these data in real-time for both competitive matches and training. Companies such as Catapult Sports and STATSports sell GPS trackers that sports teams in multiple sports across the world use to monitor their players. The type of features that are collected by these trackers include but are not limited to:
• Distance covered
• Meters per minute
• Speeds reached
• Number of sprints
• Sprints distances
• Intensity
• Time in ‘red zone’
• Accelerations
• Average metabolic power
• Heart rates
• Impacts
• Stress load
These data alongside the historical medical data that are collected by physios and club doctors can give a feature set for players who has yet to be studied by the AI community. As well as collecting other features from the club doctors and physios, we can form a list of injuries that have occurred to the players. A formal model of the problem can be stated as follows. The list of injuries that have occurred would be the target data, y. Using y, we can extract the relevant features (from a given time frame) such as Acute:Chronic Workload and the number of competitive minutes played, alongside historic data such as previous injuries to that player. This would be the feature set (X) for a prediction model, where each row in X corresponds to each injury in y. We would also need to consider examples of where no injury occurred and append these data into X and y. These data would need to be cleaned and properly structured to provide good training and test-sets when creating injury prediction models. We can then apply functions θ to these sets so that θ(X i) = y i where y i = {1, 0} with 1 corresponding to an injury and 0 corresponding to no injury. ML classification methods can be used for θ to calculate the probabilities of a player getting injured given the feature data and identify what real-world changes can be made to reduce the chances of injury.
There have been a number of studies in relation to injuries in sport which have mainly focused on the medical domain. Some relevant literatures that support the theory that AI could have a part to play in this domain are summarized in this section. There are a number of computational challenges that injury prediction presents for AI. The current literature is broken down into medical research and research that has been focused on the use of wearable sensors in sport teams.
6.1 Sports medicine research
There have been a number of studies in the Sports Medicine community focused on the causes of injuries in sports and studying a number of large datasets. Firstly, Hägglund et al. (Reference Hägglund, Waldén and Ekstrand2006) evaluate how previous injury is a risk factor for future injuries at the top level of football. The study compares two seasons (2001–2002) worth of injury data from 12 elite Swedish male football teams. They use a multivariate model to determine the relation between a previous injury and the risk it causes. They found players who were injured in the 2001 season had a greater risk of injury in the following season compared with non-injured players. Particularly, players with a previous hamstring, groin, and knee joint injuries were 2–3 times more likely to suffer the same injury in the following season. This work was extended in Hägglund et al. (Reference Hägglund, Waldén and Ekstrand2009, Reference Hägglund, Waldén and Ekstrand2013), looking at 14 football teams across Europe between 2001 and 2012. This study focused on the injury characteristics and variation of injuries during a match, season, and consecutive seasons over the time period discussed. It found that the rate of some injury types decreased over the last 11 years. However, training and match injury rates and the rates of muscle and severe injuries remain high. It was also found that the risk of injury increased with time in each half of matches. Clearly, such works point to patterns in datasets that could be used in ML algorithms to determine the risk of injury and to optimize the recovery process.
Fuller (Reference Fuller2018) models the effect of the player workloads on the injuries in the EPL. The study shows how a team’s injury-burden varies from day-to-day during a season, based on a team’s match and training schedules. It also compares successful and unsuccessful Premier League teams and how their training loads effect their number of injuries. They find that a successful team undertakes fewer training sessions each week so there are fewer opportunities in which to influence training activities and to reduce injuries. A similar study (Bowen et al. Reference Bowen, Gross, Gimpel and Li2016) investigates the relationship between physical workload and injury risk in elite youth football players. They also found higher workloads were associated with a greater injury risk. This highlights that workloads can be used as a metric in an AI model for injury prediction. Workloads have been seen as a significant factor in injury prediction, and Hullin et al. (Reference Hullin, Gabbett, Lawson, Caputi and Sampson2016) evaluate the acute:chronic workload ratio (ACWR) in Rugby League players and find that a greater ACWR increases injury risk. The ACWR is calculated by dividing the acute workload (fatigue) by the chronic workload (fitness). This is defined as:
where L is the players loadFootnote 41, t is the current day. Therefore, it is a ratio of the last 7 days load to the last 28 days load. This, along with other related variables, could be key in using ML to predict injury.
There are examples of injury studies in other sports such as basketball and American Football. In basketball, Podlog et al. (Reference Podlog, Buhler, Pollack, Hopkins and Burgess2015) survey the injuries in the NBA over a 25-year period and identify the relationship of injuries to team performance. In American Football, Ward et al. (Reference Ward, Tankovich, Ramsden, Drust and Bornn2018) find that regardless of the position, training days with high amounts of volume and intensity share an association with increased risk of injury while training days of a high amount of low intensity training share a relationship with a decreased risk of injury. Finally, Zelič et al. (Reference Zelič, Kononenko, Lavrač and Vuga1997) use decision trees and Bayesian classification to diagnose sports injuries more effectively, and this shows a novel use of ML techniques to sports injuries and provides a useful tool for teams’ doctors and physiotherapists. However, it does not aim to predict and help prevent injuries.
In the next section, we discuss the applications using the data from the wearable sensors that we discussed at the start of this section.
6.2 Wearable sensor research
Due to the amount of data that are collected from the wearable sensors, some sports teams have begun to look at ways that this can be used to benefit sports men and women. Firstly, a study Kelly et al. (Reference Kelly, Coughlan, Green and Caulfield2012) researched how wearable sensors can be used to automatically detect collisions in Rugby. As we discussed in Section 2.3, Rugby is very high impact sport and tackling is the most common cause of injury in Rugby, and therefore having a way of automatically modelling tackles can improve the work of the medical staff. The work was compared against collisions which were manually labelled using data from elite club and international level players. The paper tested a number of different algorithms for this problem such as SVMs, neural networks, and convolutional neural networks (CNN). The results show the model is able to identify collisions to a high level of accuracy, achieving a recall and precision rating of 0.933 and 0.958, respectively, using CNNs. The model can give coaching and medical staff tackle-specific measurements, in real time, which can be used in injury prevention and rehabilitation strategies. Following on from this, Cust et al. (Reference Cust, Sweeting, Ball and Robertson2018) reviewed the ways that ML and AI can be used to classify certain movements in sport.
In the next section, we will discuss the findings from this paper and highlight the computational challenges and open areas that exist for AI in the team sports domain.
7 Discussion
In this section, we discuss and highlight the open areas of research that still remain within the domain of AI for team sports. In particular, we summarize the key findings from our survey and propose a number of methods and techniques to address some of the key challenges that exist.
7.1 Match outcome prediction
Our analysis in Section 3 leads us to conclude that match outcome prediction remains a significant challenge for most team sports. To our knowledge, none of the existing work can predict match outcomes with more than 75% accuracy (see Table 5)Footnote 42.
Table 5 Current best accuracy.

These results establish benchmarks for these individual sports. However, it is not clear whether the limited prediction accuracies achieved are due to the quality of data, or whether it is due to the inherent uncertainty in the domain. To better understand what are the most important factors that determine prediction accuracy, it would be important for researchers to share their datasets, provide sensitivity analysis of their techniques, and establish what other events or features that are currently not monitored but clearly have an impact on match outcomes. For example, there are a number of factors that make it challenging to accurately predict sports match outcomes (e.g., uncertainties in team form, injuries to players, players mood, team morale, weather, playing conditions, and changes in management). Finding methods to quantify how these uncertainties will impact a game is also a challenge that could be addressed with BNs or abductive reasoningFootnote 43 that have yet to be explored. Due to the number of factors that can impact the team performance and match outcome we could use, dimensionality reduction techniques can be used to remove uninformative features and simplify the characterization of instances. If a set of the key features can be found, deep learning techniques (e.g., deep neural networks or long short term memory) could be applied effectively. Stekler et al. (Reference Stekler, Sendor and Verlander2010) explore a number of problems with prediction models in team sports and test current models against alternative forecasting methods (such as experts and the betting market) as well as examining existing biases in the models. They conclude that one area that requires further research concerns the relative weight that forecasters place on new and old information and that there is no evidence that either statistical systems or experts are able to consistently outperform the betting markets. Furthermore, Ganguly and Frank (Reference Ganguly and Frank2018) focus their attention on a number of problems when predicting teams’ performances by calculating win probabilities (many of the papers we have evaluated use win probabilities). Their results suggest that win probabilities lack sufficient context, and the models should respond to in-game factors such as injuries. They also suggest that the current win probability models should incorporate a level of uncertainty due to the many possible events and scorelines that make up the match outcome. Finally, they explore the ‘what-ifs’ in sports games and use these to model the alternative outcomes. For example, what if a team’s star player gets injured in the first half of a game, how would this affect the outcome? This highlights the fact that the majority of the current literature focuses on the final statistics of the game such as outcomes (win/loss/draw) and scorelines. In turn, there is less focus on more granular predictions which can aid the final outcome forecast. We propose the following granular approaches to the problem as follows:
• Model the problem using key match events and details to train a model that is able to recognize what outcome occurred when similar set-ups and conditions have been observed before. Deep learning techniques could be used for this approach, specifically long short term memory known as LSTMs (Hochreiter & Schmidhuber Reference Hochreiter and Schmidhuber1997), a type of RNNs which have shown to be successful in other domains when using time-series and historic datasets. Due to the vast amounts of historic datasets that are available for team sports, this approach may prove to be successful.
• Create models based on the movements of attacking and defensive units of players in order to gain a better understanding of their performances when they are facing each other in a game. This may improve on current approaches as some teams’ attacks may be more effective against specific types of defences (e.g., a blitz defence may be more successful against a running attack in American Football). Modelling the finer inter-agent interactions using multi-agent simulation techniques as in emergency evacuation prediction (Pan et al. Reference Pan, Han, Dauber and Law2007; Ramchurn et al. Reference Ramchurn, Rogers, Macarthur, Farinelli, Vytelingum, Vetsikas and Jennings2008) could potentially generate better predictions of emergent behaviours.
• Analyze the players’ personality, moods, and mental state, in the build up to games when making match outcome predictions. This would allow models to consider how player perform in certain games. For example, certain players may perform better in the finals of a competition or in fighting against relegation to a lower league, while other players may ‘choke’ and their performance will deteriorate in these types of game (Beilock & Gray Reference Beilock, Gray, Tenenbaum and Eklund2007). Natural language processing techniques (Manning & Schütze Reference Manning and Schütze1999; Sebastiani Reference Sebastiani2002; Collobert & Weston Reference Collobert and Weston2008) could thus be used to monitor pre/post-match press conferences and interviews that players give. This could also be used to analyze the managers’ confidence levels in their scheduled pre-match interviews. Another approach could be to monitor the players’ social media accounts by using sentiment analysis on their online public posts (Pang et al. Reference Pang and Lee2008). There exist numerous approaches that aim to leverage social media by means of natural language processing (Pak & Paroubek Reference Pak and Paroubek2010; Farzindar & Inkpen Reference Farzindar and Inkpen2015). However, there are some issues that arrive from this type of analysis such as not all players show up in press conferences, press conferences are often pre-prepared, and player’s social media accounts are often controlled by media managers/agents.
7.2 Strategic and tactical decision making
In Section 4 (see Figure 3), we proposed a structured framework to analyze and improve the decision-making processes in team sports. A key aspect is the recruitment of players through transfers and trading. In many cases, when a new player signs for a team, it is possible that he/she will not perform to the levels expected for the cost. This may be due to many adaptation issues based on the weather, style of play of the team, or language. Predicting the performance of a player in a new team presents an interesting ML challenge as it involves predicting with historical data that may not be completely relevant to the new team that he/she may join. Techniques for transfer learning (Pan & Yang Reference Pan and Yang2010) could potentially be used to address such issues as they have been shown to be particularly effective at learning text data across different domains. This gives an example of how we could use these techniques to map performance from one team to another which could be in different leagues and countries. The orthogonal problem to the latter involves optimizing the training process to help players reach their full potential. This is especially the case for youth players who may be at a club from an early age and where there are a number of decisions that need to be made to help them (e.g., should he/she be sent out on loan and should he/she play in the first team). Using AI to support these decisions could ensure that the best development path is selected to find the optimal results of that individual player.
Going a step further, such techniques could then be used to optimize the scouting process (where information is gathered about players before hiring them). Clubs have limited resources to perform the scouting process as well as a limited budget to purchase or train their players. This type of problem could be addressed with multi-armed bandit-based optimization techniques (Tran-Thanh et al. Reference Tran-Thanh, Stein, Rogers and Jennings2014) or sequential decision-making techniques (Beck et al. Reference Beck, Teacy, Rogers and Jennings2016) that have been successfully applied in the context of selecting workers in crowd-sourcing systems or in optimizing multi-robot teams in disaster response, respectively.
Building upon recent successes in applying game theoretic techniques (e.g., Stackelberg Games) in the security domain to defend against multiple attackers, such techniques could also be used to optimize tactics in team sports. Such techniques would need to be extended to account for the much larger number of actions and players than in traditional security games. However, the fact that sports tend to have very clearly defined payoffs and a lot of historical data to model outcomes may help in cutting down the complexity of the problem. Finally, it is worth noting that the growing popularity of E-Sports may present new opportunities to model games and team strategies as multi-agent systems.
7.3 Fantasy sports
As we discussed in Section 5, to be successful in fantasy sports there are a number of real-world and in-game factors that must be considered. These include team formation and player point prediction, changing strategies based on other competitors teams, predicting the values of players so the total value of the fantasy team is maximized, and modelling the risk of the fantasy team so that profit making strategies can be created for DFS competitions.
As well as the methods that we have described for player points prediction and team formation optimization, there are a number of other open areas within fantasy sport. Firstly, creating and running fantasy teams presents human–machine interaction challenges which include, but are not limited to: using a mixture of human knowledge and AI predictions to give ratings for the real-world players, selecting which fantasy leagues teams should be entered in to maximize profits, and exploring the problems that AI-based solutions are good at in comparison to humans. For example, it may be worth studying the affects of using an AI-based team formation approach with human player performance predictions and vice versa. This would allow us to evaluate what parts of fantasy sport games are skill and what is down to chance. This is especially important in the USA due to restrictions on gambling (Boswell Reference Boswell2008).
Finally, in DFS competitions, multiple teams can be entered into the same league by a single competitor, meaning that a portfolio of teams can be entered by a competitor to maximize their chances of winning and generating profits. This presents an interesting computational challenge to best maximize the risk and reward of competitors’ portfolios in a similar fashion to the way portfolios are treated in the financial markets. This type of strategy is discussed in Haugh and Singal (Reference Haugh and Singal2018) and could be supported by AI work using a stochastic optimization approach (Ermoliev & Wets Reference Ermoliev and Wets1988) as well as ideas from portfolio risk management strategies (Dunis et al. Reference Dunis, Middleton, Karathanasopolous and Theofilatos2016).
7.4 Injury prediction
As we showed in Section 6, sports injury prediction is an area where no significant literature exists in the AI community. Due to the negative impact that injuries can have on players careers and teams’ performance, it presents a significant new domain where AI can make a difference. The goal would be to highlight players who are likely to get injured in a given training session or a competitive match. To build these models, it would be important to use the expertise of the doctors and physiotherapists at teams to identify what new approaches and features that could be used when predicting injury. There are many sports medicine papers that suggest ACWR is related to injuries in team sports, meaning that this variable could be used as a feature in a predictive model. It is worth noting, however, that Bornn et al. (Reference Bornn, Ward and Norman2019) suggest the value of ACWR may have been over-estimated by other papers.
A key area for sports injury prediction is musculoskeletal injuries which could be prevented by changes in training load and other variables. Predictions would need to be specific to individual body parts as different features cause different injuries (e.g., turning quickly and running impact may cause knee injuries, whereas overstretching and kicking may cause hamstring injuries). This means that some methods may be better at identifying different injuries to different body parts, for example, a single model to predict hamstring injuries in footballers would be very beneficial to medical staff.
Although there has been less AI work to date in the sports domain, there is existing literature which aims to predict heart attacks and cliff edge events in the health care (Srinivas et al. Reference Srinivas, Rani and Govrdhan2010; Masethe & Masethe Reference Masethe and Masethe2014). Both of these papers use Bayesian techniques and classification algorithms to assess the risk of heart attacks and disease. This type of study could be applied to sports injuries data. If prediction models for injuries were proved to be successful, they would become a vital tool in the sporting world due to the economic and performance-based benefits that they would lead to (e.g., the financial benefits discussed in the JLT annual injury report)Footnote 11.
7.5 Places to publish
It is worth highlighting a few major journals and conferences which fall outside of the sports domain, which have attracted sports-related articles. These include but are not limited to: IEEE transactions in Cybernetics, IEEE Trans on TPAMI, Trans on Knowledge and Data Engineering, IEEE Trans on Neural Networks and Learning Systems. This shows the wider use of the sports as a tool to improve scientific processes and AI.
Some options of publications directly in the sports domain are as follows: Sports Engineering, International Journal of Computer Science in Sport, MIT Sloan Sports Analytics Conference, Journal of Sports Analytics, Journal of Quantitative Analysis in Sports, New England Symposium on Statistics in Sports, Workshop on Sports Analytics (ECML/PKDD), and Workshop on AI in Team Sports (AAAI). This is also summarized in Swartz (Reference Swartz2018).
8 Conclusions
This paper has evaluated the questions that exist for the AI community in the team sports domain and has provided a structured framework for future work. We have identified a number of key research areas to give a comprehensive overview of the work to date and open areas for future work. We have also demonstrated the potential to create a unique real-world live testbed for AI and ML techniques to be validated in the future. In particular, we reviewed the works for match outcome prediction and found that due to the unpredictability of sports, the models still fail to predict outcomes significantly better than the bookmakers and appear to reach a glass ceiling. However, we identified a number of possible methods to improve current work and break the glass ceiling. We outlined a number of key decision-making processes in the team sports domain. We then discussed the existing possibilities for applications of AI techniques to improve these processes and compared the problems posed to existing AI literature in other domains. We also reviewed the literature in the fantasy sports domain and found that AI techniques have been applied to significantly outperform the majority of human players in the FPL competition for football. However, there are areas in the fantasy sport process where AI could be applied to further improve fantasy prediction and devise betting strategies. Finally, we focused on the use of AI in injury prediction and found that there has been no significant work by the AI community. However, there are a number of interesting Sports Medicine papers that highlight the possible features and data that could be used to build prediction models. This is supported by the existing AI literature in the health care industry using techniques to predict heart attacks (Srinivas et al. Reference Srinivas, Rani and Govrdhan2010; Masethe & Masethe Reference Masethe and Masethe2014). Overall this paper highlights the impacts that AI and ML methods could have on the team sports domain, outlining a number of processes where there are existing open areas and research questions.
Acknowledgements
We would like to thank Dr. Tim Matthews and Mr. Ramm Mylvagananam for their expert advice and comments while writing this paper. This research is sponsored by the EPSRC NPIF doctoral training grant number EP/S515590/1.













