Article contents
Oscillation of differential equations with non-monotone retarded arguments
Published online by Cambridge University Press: 01 March 2016
Abstract
Consider the first-order retarded differential equation 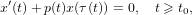 $$\begin{eqnarray}x^{\prime }(t)+p(t)x({\it\tau}(t))=0,\quad t\geqslant t_{0},\end{eqnarray}$$
$$\begin{eqnarray}x^{\prime }(t)+p(t)x({\it\tau}(t))=0,\quad t\geqslant t_{0},\end{eqnarray}$$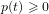 $p(t)\geqslant 0$ and
$p(t)\geqslant 0$ and 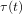 ${\it\tau}(t)$ is a function of positive real numbers such that
${\it\tau}(t)$ is a function of positive real numbers such that 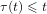 ${\it\tau}(t)\leqslant t$ for
${\it\tau}(t)\leqslant t$ for 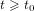 $t\geqslant t_{0}$ , and
$t\geqslant t_{0}$ , and 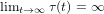 $\lim _{t\rightarrow \infty }{\it\tau}(t)=\infty$ . Under the assumption that the retarded argument is non-monotone, a new oscillation criterion, involving
$\lim _{t\rightarrow \infty }{\it\tau}(t)=\infty$ . Under the assumption that the retarded argument is non-monotone, a new oscillation criterion, involving 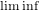 $\liminf$ , is established when the well-known oscillation condition
$\liminf$ , is established when the well-known oscillation condition 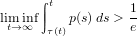 $$\begin{eqnarray}\liminf _{t\rightarrow \infty }\int _{{\it\tau}(t)}^{t}p(s)\,ds>\frac{1}{e}\end{eqnarray}$$
$$\begin{eqnarray}\liminf _{t\rightarrow \infty }\int _{{\it\tau}(t)}^{t}p(s)\,ds>\frac{1}{e}\end{eqnarray}$$
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2016
References
- 3
- Cited by

