1. Introduction
The radiative lifetime of excess charge carriers is a fundamental property of semiconductor structures, which has important implications for device operation. Quantum wells from the group-III nitrides are particularly interesting for their potentially very large free exciton binding energy, making excitons stable up to rather high temperatures. Even for bulk GaN, the radiative lifetime of excess carriers is dominated by free excitons up to room temperature Reference Hangleiter, Im, Forner, Härle and Scholz[1]. Due to the localization of carriers in the quantum wells, the exciton Bohr radius is expected to shrink and the radiative lifetime to reduce.
For other III-V semiconductor quantum wells, the radiative decay of carriers has been studied in some detail. Feldmann et al. Reference Feldmann, Peter, Göbel, Dawson, Moore, Foxon and Elliott[2] have shown that, above some critical temperature, the radiative exciton lifetime in GaAs/AlGaAs quantum wells increases linearly with temperature. Michler et al. Reference Michler, Hangleiter, Moritz, Härle and Scholz[3] have demonstrated the influence of exciton dissociation on the radiative decay time in GaInAs/InP quantum wells.
We have studied the radiative lifetime in GaInN/GaN single quantum wells using picosecond time resolved photoluminescence spectroscopy.
2. Experimental
2.1 Samples
Our samples were grown on 0001 oriented sapphire substrates using low pressure metal-organic vapor phase epitaxy (LP-MOVPE) and employing an AlN buffer layer. The growth temperature for GaN was about 1000°C, whereas GaInN was grown at about 800°C. Thick GaN samples exhibited X-ray diffraction linewidths of 50- 80 arcsecs and photoluminescence linewidths of around 2-4 meV. The net donor concentration of nominally undoped GaN was less than 1 × 1017cm3. For the quantum wells, we used a 500nm GaN buffer and a 200nm GaN cap layer. The thickness of the GaInN quantum wells was varied between 0.6nm and 20nm.
2.2 Measurement setup
The carrier dynamics were investigated using a picosecond time-resolved photoluminescence setup, where the samples were excited with 5ps pulses from a cavity-dumped frequency-doubled synchronously mode-locked dye laser. The luminescence was detected with a Hamamatsu R3809U microchannel-plate photomultiplier and processed using time- correlated single-photon-counting electronics. By employing suitable deconvolution techniques, an overall time resolution of less than 20ps was reached. The samples were mounted in a variable-temperature cryostat, allowing for a temperature range from 2K up to 400K.
3. Experimental results
Measurements of the photoluminescence (PL) decay time as well as of the integrated PL intensity were performed for temperatures between 5K and 300K. The PL spectra exhibit a low temperature linewidth of the QW emission of about 80meV, as shown in Figure 1. The QW emission shifts to lower energy at higher temperatures due to bandgap shrinkage, but retains it overall shape. Figure 2 shows typical measured PL decay traces for various temperatures, where a clearly exponential decay is observed. As shown in Figure 3 for a 1.2nm quantum well, the decay time is about 600ps at low temperature and is approximately constant up to about 20K. For temperatures above 50K, the decay time decreases sharply, reaching about 75ps at room temperature. The decrease of the decay time at elevated temperatures is associated with an activation energy of about 30meV. By measuring the integrated PL intensity as a function of temperature, we obtain an at least relative measure for the quantum efficiency of the band edge emission. Figure 4 shows the results for the temperature range 5K to 300K. Similar to the temperature dependence of the PL decay time, the integrated intensity is constant below 20K and decreases sharply above about 100K. This indicates that at elevated temperatures, electron-hole pairs (excitons) are transfered into nonradiative states, at least under our experimental conditions. By combining our data for the decay time, which is due to both radiative and nonradiative processes, with the data for the quantum efficiency η, we obtain the radiative lifetime according to
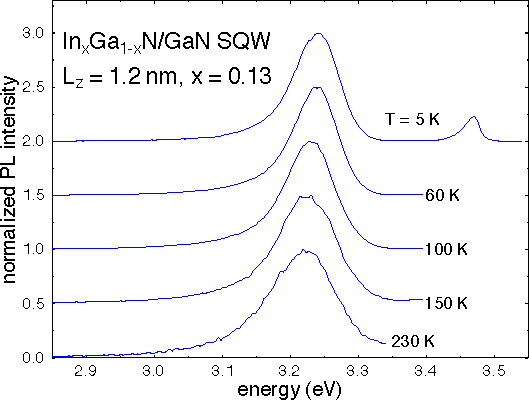
Figure 1. Photoluminescence spectra at various temperatures of a InGaN/GaN quantum well sample. The quantum well emission is at about 3.23 eV, whereas the GaN barrier emits at about 3.47 eV.
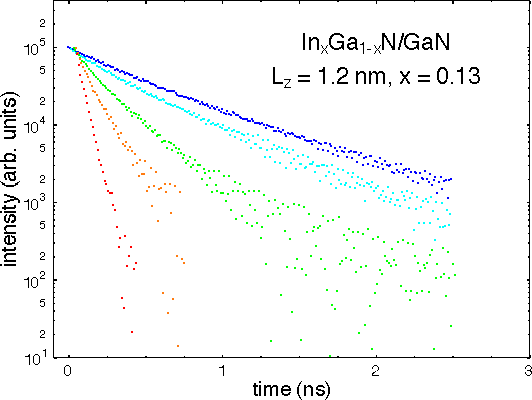
Figure 2. Typical photoluminescence decay traces for a GaInN/GaN single quantum well for various temperatures. The decay gets faster at higher temperatures.

Figure 3. Measured photoluminescence decay time for a 1.2 nm GaInN/GaN single quantum well as a function of temperature.

Figure 4. Integrated photoluminescence intensity versus temperature. Assuming unity quantum efficiency at low temperature, this corresponds to the temperature dependence of the quantum efficiency.
Rigorously speaking, this is only a lower bound for the radiative lifetime, since the integrated PL intensity provides only for an upper bound of the quantum efficiency. The results for the radiative lifetime versus temperature are shown in Figure 5.
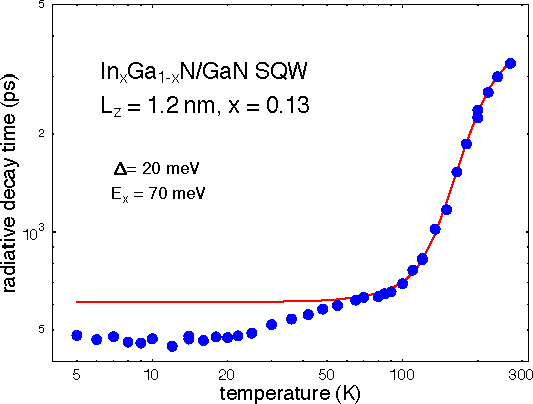
Figure 5. Radiative exciton lifetime vs. temperature. The radiative lifetime is calculated from the measured decay time and the quantum efficiency. The full line is explained in the text.
4. Discussion
In a very simplistic model, the radiative lifetime of free excitons in quantum well structures would be proportional to the temperature. This is due to the fact that k conservation requires that only excitons with a center-of-mass wavevector of zero (more precisely: equal to the photon wavevector) can recombine radiatively. Since the excitons are distributed thermally among their density of states according to a Boltzmann distribution, the resulting radiative lifetime is proportional to T.
However, there are several effects making the real picture more complicated. First of all, excitons may get localized at low temperature due to potential fluctuations due to either alloy fluctuations or to well thickness variations. The localization is equivalent to a spreading of the exciton wavefunction in k space and to a reduced radiative rate at low temperature. Moreover, if sufficient thermal energy is available, excitons may get dissociated into free electrons and holes at elevated temperatures. Since free electrons and holes at low carrier density have a lower radiative recombination probability, this leads to an enhanced increase of the radiative lifetime at high temperature.
In order to describe these effects in a quantitative manner, we use a combination Reference Michler, Hangleiter, Moritz, Härle and Scholz[3] of the models of Feldmann et al. Reference Feldmann, Peter, Göbel, Dawson, Moore, Foxon and Elliott[2] at low temperature and Ridley Reference Ridley[4] for exciton dissociation. A fit of our data for the radiative lifetime based on this model yields the full line shown in Figure 5, which is in excellent agreement with the experimental data. The fitting procedure also provides estimates for a number of interesting parameters, including the exciton binding energy Ex and the localization parameter Δ. We find Ex ≈ 70meV and λ ≈ 20 meV. For the exciton binding energy, this means that it is about doubled com pared to bulk GaN, which is reasonable for quantum wells with a thickness of about half the bulk exciton Bohr radius. The localization of about 20 meV is rather strong, explaining the unexpectedly large low temperature lifetime of the excitons.
It is surprising to note that the radiative lifetime of excitons in GaInN/GaN quantum wells at low temperatures is much longer than the free exciton lifetime in bulk GaN at the same temperature. This can be attributed to the fact that localization of the excitons seems to play a major role in the nitride quantum wells. Localization leads to a reduced number of K=0 excitons and therefore to a large radiative lifetime. There are two primary reasons for this. First of all, due to the large effective masses of electrons and holes in the nitrides, the quantum wells have to be rather thin in order to exhibit sizeable quantization effects, leading to a large effect of well width fluctuations. Secondly, from the technological point of view, it is well known that In incorporation in the nitrides during epitaxial growth is a problem, and consequently it is likely that there is a relatively large fluctuations of the In content, leading to localization in areas of larger In content. Only at elevated temperatures the thermal distribution of the excitons becomes more extended in K space than the localization-induced exciton wavefunction so that the average occupation at K=0 is reduced compared to low temperature. At these temperatures, there is also a partial dissociation of the excitons into free electrons and holes. Since the free exciton binding energy is rather large even in bulk GaN (≈30 meV Reference Merz, Kunzer and Kaufmann[5]), we expect a giant exciton binding energy in thin quantum wells, where the exciton binding energy should ideally be increased by a factor of four. This should lead to a high thermal stability of the excitons.
The real measured decay time of the excitons in the quantum wells decreases rather than increases at elevated temperatures. This is commonly interpreted as an indication of nonradiative processes coming into play. However, due to the strong influence of localization under our conditions, we have to be somewhat cautious about this. If a large fraction of excitons is localized at potential fluctuations at low temperature, an increase in thermal energy will free these excitons and allow them to diffuse to either non-radiative centers or to trapping sites like donor-acceptor pairs, where the excitons get lost for the radiative band-edge emission.
5. Summary
We have studied the decay of excitons in GaInN/GaN quantum wells. From measurements of the photoluminescence decay time and of the photoluminescence efficiency we have derived the radiative lifetime of excitons in these structures as a function of temperature. The observed temperature dependence of the radiative lifetime is explained by localization of excitons at low temperature and by thermal dissociation of excitons at temperatures in excess of 100 K. The real decay time of the excitons is strongly influenced by trapping or non-radiative recombination.






