Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Podestá, Ricardo A.
2023.
Geometric Proofs that √3, √5 and √7 are Irrational.
Mathematics Magazine,
Vol. 96,
Issue. 1,
p.
34.


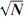 is irrational
is irrational