Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T10:58:37.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Application of Mathieu's Equation to Stability of Non-Linear Oscillator

Published online by Cambridge University Press:  03 November 2016

N. W. McLachlan
Get access Rights & Permissions [Opens in a new window]

Extract

The differential equation for y, the lateral displacement of an electrically-driven tuning fork, is

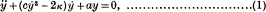
where a>0, c, κ small>0. (cẏ2-2κ), the coefficient in the damping term, is positive or negative according as cẏ2>2κ or cẏ2<2κ. During periodic motion, the coefficient changes sign, such that the inherent loss per period is compensated exactly by the energy supplied from the driving agent. In the language of “electronics”, loss corresponds to a “positive” resistance and energy supply to a “negative” resistance, both of which vary periodically.

Type
Research Article
Information
The Mathematical Gazette , Volume 35 , Issue 312 , May 1951 , pp. 105 - 107
Copyright
Copyright © The Mathematical Association 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Rayleigh, , Phil. Mag., 15, 229, 1883.CrossRefGoogle Scholar

† McLachlan, , Ordinary Non-linear Differential Equations (Oxford, 1950),Google Scholar which will be designated by N.D.E.

* McLachlan, , Mathieu Functions (Oxford, 1947),Google Scholar designated by M.F.