The Farey series of order n, Fn, consists of all the fractions between 0 and 1 (inclusive) with denominators less than or equal to n, arranged in order of magnitude and expressed in their lowest terms, so that for example 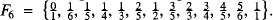The most obvious way of computing one is to assign a long series of stores and then insert the terms with denominator 1, with denominator 2, … , shifting the terms already there to make room for the new ones in their correct positions. This may require a large amount of storage and is fairly slow because of the large amount of shifting involved: for instance F1025 has 319765 terms, and occupies 400 printed pages (see Neville [1]). Neville also gives a table related to F100, which has 3045 terms. His procedures, a heroic application of pencil-and-paper methods, are described at the end of this paper.