Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T21:21:26.032Z Has data issue: false hasContentIssue false
  • English
  • Français

Forming groups with 4 × 4 matrices

Published online by Cambridge University Press:  23 January 2015

J. R. Harris
J. R. Harris*
Affiliation:
6 Willowdene Court, Bembridge PO35 5SS
Get access Rights & Permissions [Opens in a new window]

Extract

The three Pauli matrices are normally given [1] as the 2 × 2 matrices:

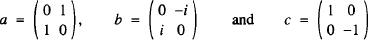
where ‘i’ is the usual complex number imaginary unit.

These matrices obey the relations a2 = I = b2 = c2(where I is the 2 × 2 identity matrix), as well as the anticommutation relations:

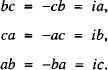
Within the quantities ia,ib and ic,i is a scalar multiplier of the 2 × 2 Pauli matrices and, of course, commutes with each of a, b, c.

Type
Articles
Information
The Mathematical Gazette , Volume 94 , Issue 531 , November 2010 , pp. 426 - 429
Copyright
Copyright © The Mathematical Association 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Maxwell, E. A., Algebraic structure and matrices, Cambridge University Press (1965) p. 192.Google Scholar
2. Copson, E. T., Theory of functions of a complex variable, Oxford University Press (1935) pp. 1–5.Google Scholar
3. Sawyer, W. W., A path to modern mathematics, Penguin (1966) p. 142.Google Scholar
4. Ledermann, W., Introduction to the theory of finite groups (4th edn.), Oliver & Boyd (1961).Google Scholar