Article contents
Graph-theoretic models for the Fibonacci family
Published online by Cambridge University Press: 23 January 2015
Extract
The well-known Fibonacci and Lucas numbers continue to faxcinate the mathematical community with their beauty, elegance, ubiquity, and applicability. After several centuries of exploration, they are still a fertile ground for additional activities, for Fibonacci enthusiasts and amateurs alike.
Fibonacci numbers Fn and Lucas numbers Ln belong to a large integer family {xn}, often defined by the recurrence xn = xn−1 + xn−2, where x1 = a, x2 = b, and n ≥ 3. When a = b = 1, xn = Fn; and when a = 1 and b = 3, xn = Ln. Clearly, F0 = 0 and L0 = 2. They satisfy a myriad of elegant properties [1,2,3]. Some of them are:
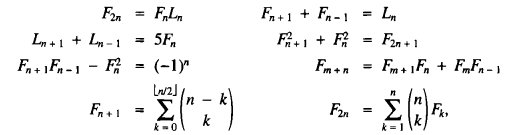
In this article, we will give a brief introduction to the Q-matrix, employ it in the construction of graph-theoretic models [4, 5], and then explore some of these identities using them.
In 1960 C.H. King studied the Q-matrix
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2014
References
- 4
- Cited by

