Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T10:57:27.156Z Has data issue: false hasContentIssue false
  • English
  • Français

A modern look at a neglected summation formula by Euler

Published online by Cambridge University Press:  01 August 2016

Thomas J. Osler  and
Walter Jacob
Thomas J. Osler
Affiliation:
Mathematics Department, Rowan University, Glassboro, NJ 08028, USA email: osler@rowan.edu
Walter Jacob
Affiliation:
Mathematics Department, Rowan University, Glassboro, NJ 08028, USA email: osler@rowan.edu
Get access Rights & Permissions [Opens in a new window]

Extract

In Euler derives the approximate summation formula

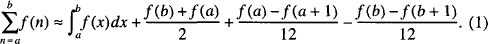
This primitive result does not appear to be well known to modern readers, and we will try to show by examples that it deserves more attention. After translating this paper into English and reflecting on its contents, we thought it desirable to present Euler’s work in a form convenient for today’s readers. Because of inadequate notations for functions, sums, and definite integrals, the modern reader is likely to find Euler’s writing difficult, even in translation. Also, in Euler’s time, mathematicians were familiar with properties of the conic sections that have largely been ignored today.

Type
Articles
Information
The Mathematical Gazette , Volume 93 , Issue 527 , July 2009 , pp. 237 - 243
Copyright
Copyright © The Mathematical Association 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Euler, L., Methodus universalis serierum convergentium summas quam proxime inveniendi, (A general method for finding approximations to the sums of convergent series (E46)), originally published in Commentarii academiae scientiarum Petropolitanae 8, (1741) pp. 3–9. Opera Omnia: Series 1, Volume 14, pp. 101-107. A translation with notes by Jacob, W. and Osier, T.J. is available on the web at the Euler Archive, http://www.math.dartmouth.edu/~euler/.Google Scholar
2. Knopp, Konrad, Theory and application of infinite series, Dover Publications, New York, 1990 (a translation by R. C. H. Young of the 4th German addition of 1947).Google Scholar
3. Lowry, H.V., Elementary derivation of the Euler-Maclaurin summation formula, Math. Gaz. 31 (Oct. 1947) pp. 248–249.CrossRefGoogle Scholar