In this paper we show how to derive Vieta’s famous product of nested radicals for π [1] from the Archimedean iterative algorithm for π, [2, 3]. Only simple algebraic manipulations are needed.

The Archimedean iterative algorithm for calculating π uses a method involving the two equations:

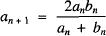
and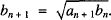

In using this algorithm, we start with a circle of diameter 1. Imagine two regular polygons each with the same number of sides, circumscribed and inscribed to this circle. The larger one has perimeter a0, the smaller has perimeter b0. Since the perimeter of the circle is π we have b0 < π < a0. Now consider regular polygons with twice the number of sides that circumscribe and inscribe the circle and call their perimeters a1 and b1 respectively. These can be calculated from (1) and (2). Continuing in this way we generate the perimeters of inscribed and circumscribed regular polygons, and in each case the number of sides is twice the sides of the previous polygon. Clearly the sequence {an} approaches π from above and {bn} approaches π from below.