Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-16T11:22:52.612Z Has data issue: false hasContentIssue false
  • English
  • Français

The main body of some irrational complex functions

Published online by Cambridge University Press:  01 August 2016

Irena Kosi-Ulbl
Irena Kosi-Ulbl*
Affiliation:
Faculty of Education, University of Maribor, Koroška c. 160, 2000 Maribor, Slovenia. e-mail: Irena.Kosi@uni-mb.si
Get access Rights & Permissions [Opens in a new window]

Extract

We suggest a way to make traditional geometry more interesting for students. Investigating the connection between classical geometry and modern chaos theory seems to be a suitable way of motivating them. Excursions into complex number iterations and interesting Mandelbrot sets offer many methods of discovering and exploring.

In H. Zeitler considers the complex function 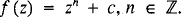The classic case n = 2 was investigated by Mandelbrot. We are discussing a more general case where the exponent n is a rational number.

Type
Articles
Information
The Mathematical Gazette , Volume 85 , Issue 502 , March 2001 , pp. 42 - 49
Copyright
Copyright © The Mathematical Association 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Zeitler, H., About iterations of special complex functions, Leaflets in Mathematics, Janus Pannonius University, Pecs (1996).Google Scholar
2. Peitgen, H.-O., Richter, P. H., The beauty of fractals, Springer (1986).CrossRefGoogle Scholar