No CrossRef data available.
Article contents
Reciprocally related primes
Published online by Cambridge University Press: 12 November 2024
Extract
Number theory and especially primes are an infinite source of inspirational ideas in elementary mathematics. Many of these ideas can be understood and some also explained with very basic mathematical knowledge. In our paper we explain the cycle which appears between the first six multiples of the decimal expression of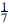 and explore an inspiringly simple relation between primes, which somehow makes them gather into mysterious groups. And while exploring these simple questions, we are led to unveil some aspects of the power and limits of human mind and those of a computer.
and explore an inspiringly simple relation between primes, which somehow makes them gather into mysterious groups. And while exploring these simple questions, we are led to unveil some aspects of the power and limits of human mind and those of a computer.
Information
- Type
- Articles
- Information
- Copyright
- © The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association
References
Tattersall, J. J., Elementary number theory in nine chapters (2nd edn.) Cambridge (2005).CrossRefGoogle Scholar
RSA numbers, Wikipedia, accessed April 2024 at https://en.wikipedia.org/wiki/RSAnumbers
Google Scholar
The Cunningham Project, accessed April 2024 at https://homes.cerias.purdue.edu/∼ssw/cun/
Google Scholar
Kobal, Damjan, Factorisation of 101540 – 1, accessed March 2024 at https://ko.fmf.uni-lj.si/fact/Factor-10-to-1540-1.pdf
Google Scholar


