Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T22:33:43.940Z Has data issue: false hasContentIssue false
  • English
  • Français

The tables of John Wallis and the discovery of his product π

Published online by Cambridge University Press:  23 January 2015

Thomas J. Osler
Thomas J. Osler*
Affiliation:
Dept. of Mathematics, Rowan University, Glassboro, NJ 08028 USA, e-mail: osler@rowan.edu
Get access Rights & Permissions [Opens in a new window]

Extract

In the year 1656 John Wallis published his Arithmetica Infinitorum, [1], in which he displayed many ideas that were to lead to the integral calculus of Newton. In this work we find the celebrated infinite product of Wallis which gives π,

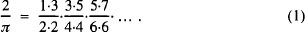
Earlier in 1593, Vieta [2] found another infinite product which gives π

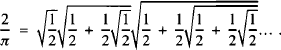
But, since Wallis does not mention it, we suppose that he was unaware of it. (Remarkably, these two seemingly different products are special cases of a more general formula [3].)

Type
Articles
Information
The Mathematical Gazette , Volume 94 , Issue 531 , November 2010 , pp. 430 - 437
Copyright
Copyright © The Mathematical Association 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Wallis, John, The arithmetic of infinitesimals (translated from Latin by Stedall, Jacqueline A.), Springer Verlag (2004).10.1007/978-1-4757-4312-8Google Scholar
2. Vieta, F., Variorum de Rebus Mathematicis Reponsorum Liber VII, (1593) in: Opera Mathematica, (reprinted) Georg Olms Verlag, Hildesheim, New York, 1970, pp. 398-400, 436–446.Google Scholar
3. Osler, T. J., The united Vieta's and Wallis' products for π, Amer. Math. Monthly, 106 (1999) pp. 774–776.10.1080/00029890.1999.12005119Google Scholar
4. Nunn, T. Percy, The arithmetic of infinites: A school introduction to the integral calculus (Part 1), Math. Gaz., 5 (1910) pp. 345–356.Google Scholar
5. Nunn, T. Percy, The arithmetic of infinites: A school introduction to the integral calculus (Part 2), Math. Gaz., 5 (1911) pp. 377–386.10.2307/3604913Google Scholar
6. Stedall, Jacqueline A., Catching Proteus: The collaborations of Wallisc and Brouncker. I. Squaring the circle, Notes and Records of the Royal Society of London, 54 (3) (September 2000) pp. 293–316.10.1098/rsnr.2000.0114Google Scholar
7. Dutka, J., Wallis' product, Brouncker's continued fraction, and Leibniz's series, Arch. History Exact Sciences 26 (1982), pp. 115–126.10.1007/BF00348349Google Scholar