Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Delbourgo, Daniel
and
Ward, Tom
2008.
Non-abelian congruences between L-values of elliptic curves.
Annales de l'Institut Fourier,
Vol. 58,
Issue. 3,
p.
1023.
Bley, Werner
2011.
Numerical Evidence for the Equivariant Birch and Swinnerton-Dyer Conjecture.
Experimental Mathematics,
Vol. 20,
Issue. 4,
p.
426.
WARD, THOMAS
2012.
Congruences for convolutions of Hilbert modular forms.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 153,
Issue. 3,
p.
471.
KIM, DOHYEONG
2013.
p-adic L-functions over the false Tate curve extensions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 155,
Issue. 3,
p.
483.
DELBOURGO, DANIEL
and
PETERS, LLOYD
2015.
HIGHER ORDER CONGRUENCES AMONGST HASSE–WEIL -VALUES.
Journal of the Australian Mathematical Society,
Vol. 98,
Issue. 1,
p.
1.
DELBOURGO, DANIEL
and
LEI, ANTONIO
2016.
Non-commutative Iwasawa theory for elliptic curves with multiplicative reduction.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 160,
Issue. 1,
p.
11.
Evans, Robert
Macias Castillo, Daniel
and
Wiersema, Hanneke
2025.
Numerical Evidence for a Refinement of Deligne’s Period Conjecture for Jacobians of Curves.
Experimental Mathematics,
Vol. 34,
Issue. 3,
p.
366.
Angdinata, David Kurniadi
2025.
On L-values of elliptic curves twisted by cubic Dirichlet characters.
Canadian Journal of Mathematics,
p.
1.

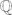 , and τ an Artin representation over
, and τ an Artin representation over 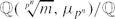 , where
, where 