Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T03:19:45.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of free nilpotent-by-abelian groups

Published online by Cambridge University Press:  24 October 2008

R. M. Bryant  and
C. K. Gupta
R. M. Bryant
Affiliation:
University of Manchester Institute of Science and Technology, Manchester M60 1QD
C. K. Gupta
Affiliation:
University of Manitoba, Winnipeg R3T 2N2, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

Let Fn be a free group of finite rank n with basis {x1,…, xn}. Let 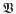be a variety of groups and write 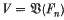for the verbal subgroup of Fn corresponding to 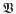. (See [11] for information on varieties and related concepts.) Every automorphism of Fn induces an automorphism of the relatively free group Fn/V, and those automorphisms of Fn/V arising in this way are called tame. If 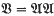is the variety of all metabelian groups and n ╪ 3 then every automorphism of Fn/V is tame [2, 4, 12]. But this is an exceptional situation. For many (and probably most) other varieties 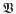, Fn/V has non-tame automorphisms for all sufficiently large n. This holds for the variety 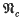of all nilpotent groups of class at most c where c ≥ 3 [1, 3] and for nearly all product varieties 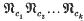including, in particular, the variety 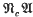of all groups whose derived groups are nilpotent of class at most c, where c > 2 [10, 13].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 114 , Issue 1 , July 1993 , pp. 143 - 147
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andreadakis, S.. On the automorphisms of free groups and free nilpotent groups. Proc. London Math. Soc. (3) 15 (1965), 239–268.CrossRefGoogle Scholar
[2]Bachmuth, S.. Automorphisms of free metabelian groups. Trans. Amer.Maih. Soc. 118 (1965), 93–104.CrossRefGoogle Scholar
[3]Bachmuth, S.. Induced automorphisms of free groups and free metabelian groups. Trans. Amer. Math. Soc. 122 (1966), 1–17.CrossRefGoogle Scholar
[4]Bachmuth, S. and Mochizuki, H. Y..Aut(F)→Aut(F/Fn) is surjective for free group F of rank ≥ 4. Trans. Amer. Math. Soc. 292 (1985), 81–101.Google Scholar
[5]Bryant, R. M. and Geoves, J. R. J.. On automorphisms of relatively free groups. J. Algebra 137 (1991), 195–205.CrossRefGoogle Scholar
[6]Bryant, R. M. and Groves, J. R. J.. Automorphisms of free metabelian groups of infinite rank. Comm. Algebra 20 (1992), 783–814.CrossRefGoogle Scholar
[7]Bryant, R. M. and Macedonska, O.. Automorphisms of relatively free nilpotent groups of infinite rank. J. Algebra 121 (1989), 388–398.CrossRefGoogle Scholar
[8]Gupta, C. K. and Gupta, N. D.. Lifting primitivity of free nilpotent groups. Proc. Amer. Math. Soc. 114 (1992), 617–621.CrossRefGoogle Scholar
[9]Gupta, C. K., Gupta, N. D. and Roman'kov, V. A.. Primitivity in free groups and free metabelian groups. Canad. J. Math. 44 (1992), 516–523.CrossRefGoogle Scholar
[10]Gupta, C. K. and Levin, F.. Tame range of automorphism groups of free polynilpotent groups. Comm. Algebra 19 (1991), 2497–2500.CrossRefGoogle Scholar
[11]Neumann, H.. Varieties of groups (Springer, Berlin, 1967).CrossRefGoogle Scholar
[12]Roman'kov, V. A.. Automorphism groups of free metabelian groups. Problems of Relationships of Abstract and Applied Algebra (Novosibirsk, 1985), 53–80.Google Scholar
[13]Shpilrain, V. E.. Automorphisms of F/R' groups. Internat. J. Algebra and Comput. 1 (1991), 177–184.CrossRefGoogle Scholar