Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gupta, K. C.
and
Goyal, S. P.
1971.
On Generating Functions for a New Class of Polynomials.
Mathematische Nachrichten,
Vol. 51,
Issue. 1-6,
p.
43.
Lahiri, Maya
and
Satyanarayana, Bavanari
1995.
Certain bilateral generating relations for generalized hypergeometric functions.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 105,
Issue. 3,
p.
297.

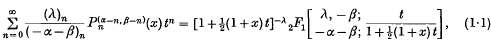
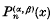 is defined as ((5), p. 255)
is defined as ((5), p. 255)