Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T03:25:36.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds on fewnomial exponential sums over ℤp

Published online by Cambridge University Press:  22 June 2010

TODD COCHRANE  and
CHRISTOPHER PINNER
TODD COCHRANE
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66506, U.S.A. e-mail: cochrane@math.ksu.edu, pinner@math.ksu.edu
CHRISTOPHER PINNER
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66506, U.S.A. e-mail: cochrane@math.ksu.edu, pinner@math.ksu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain a number of new bounds for exponential sums of the type S(χ, f) = ∑x = 1p−1 χ(x) ep(f(x)), with p a prime, f(x) = ∑i = 1raixki, ai, ki ∈ ℤ, 1 ≤ i ≤ r and χ a multiplicative character (mod p). The bounds refine earlier Mordell-type estimates and are particularly effective for polynomials in which a certain number of the ki have a large gcd with p − 1. For instance, if f(x) = ∑i = 1maixki + g(xd) with d|(p − 1) then 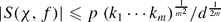. If f(x) = axk + h(xd) with d|(p − 1) and (k, p − 1) = 1 then 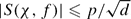, and if f(x) = axk + bx−k + h(xd) with d|(p − 1) and (k, p − 1) = 1 then .

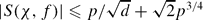Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 149 , Issue 2 , September 2010 , pp. 217 - 227
Copyright
Copyright © Cambridge Philosophical Society 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Akuliničev, N. M.Estimates for rational trigonometric sums of a special type. Dokl. Acad. Sci. USSR 161 (1965), 743–745. English trans in Doklady 161, no. 4 (1965), 480–482.Google Scholar
[2]Bourgain, J. Some arithmetical applications of the sum-product theorems in finite fields. Geometric aspects of functional analysis. 99–116, Lecture Notes in Math. 1910 (Springer, 2007).CrossRefGoogle Scholar
[3]Castro, F. N. and Moreno, C. J.Mixed exponential sums over finite fields. Proc. Amer. Math. Soc. 128, no. 9 (2000), 2529–2537.CrossRefGoogle Scholar
[4]Cochrane, T. and Pinner, C.An improved Mordell type bound for exponential sums. Proc. Amer. Math. Soc. 133 (2005), no. 2, 313–320.CrossRefGoogle Scholar
[5]Cochrane, T., Coffelt, J. and Pinner, C.A further refinement of Mordell's bound on exponential sums. Acta Arith. 116 (2005), no. 1, 35–41.CrossRefGoogle Scholar
[6]Cochrane, T., Coffelt, J. and Pinner, C.A system of simultaneous congruences arising from trinomial exponential sums. J. Théor. Nombres Bordeaux 18 (2006), no. 1, 59–72.CrossRefGoogle Scholar
[7]Kloosterman, H. D.On the Representation of Numbers in the Form ax 2 + by 2 + cz 2 + dt 2. Acta Math. 49 (1926), 407–464.CrossRefGoogle Scholar
[8]Mordell, L. J.On a sum analagous to a Gauss's sum. Quart. J. Math. 3 (1932), 161–167.CrossRefGoogle Scholar
[9]Perel'muter, G. I.Estimate of a sum along an algebraic curve. Mat. Zametki 5 (1969), 373–380.Google Scholar
[10]Weil, A.On some exponential sums. Proc. Nat. Acad. Sci. U.S.A. 34 (1948), 204–207.CrossRefGoogle ScholarPubMed
[11]Wooley, T. D.A note on simultaneous congruences, II: Mordell revised. J. Aust. Math. Soc. 88 (2010), 261–275.CrossRefGoogle Scholar
[12]Yu, H. B.Estimates for complete exponential sums of special types. Math. Proc. Cam. Phil. Soc. 131 (2001), no. 2, 321–326.CrossRefGoogle Scholar