Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vaintrob, A.
1996.
Universal weight systems and the Melvin-Morton expansion of the colored Jones knot invariant.
Journal of Mathematical Sciences,
Vol. 82,
Issue. 1,
p.
3240.
Rozansky, L.
1997.
Higher order terms in the Melvin-Morton expansion of the colored Jones polynomial.
Communications in Mathematical Physics,
Vol. 183,
Issue. 2,
p.
291.
Lin, Xiaosong
and
Wang, Zhenghan
1999.
On ohtsuki’s invariants of integral homology 3-spheres.
Acta Mathematica Sinica,
Vol. 15,
Issue. 3,
p.
293.
Murakami, Hitoshi
and
Murakami, Jun
2001.
The colored Jones polynomials and the simplicial volume of a knot.
Acta Mathematica,
Vol. 186,
Issue. 1,
p.
85.
Kashaev, R. M.
and
Tirkkonen, O.
2003.
Proof of the Volume Conjecture for Torus Knots.
Journal of Mathematical Sciences,
Vol. 115,
Issue. 1,
p.
2033.
Hikami, Kazuhiro
2003.
Volume Conjecture and Asymptotic Expansion ofq-Series.
Experimental Mathematics,
Vol. 12,
Issue. 3,
p.
319.
Hikami, Kazuhiro
and
Kirillov, Anatol N.
2003.
Torus knot and minimal model.
Physics Letters B,
Vol. 575,
Issue. 3-4,
p.
343.
MURAKAMI, HITOSHI
2004.
ASYMPTOTIC BEHAVIORS OF THE COLORED JONES POLYNOMIALS OF A TORUS KNOT.
International Journal of Mathematics,
Vol. 15,
Issue. 06,
p.
547.
HIKAMI, KAZUHIRO
2004.
DIFFERENCE EQUATION OF THE COLORED JONES POLYNOMIAL FOR TORUS KNOT.
International Journal of Mathematics,
Vol. 15,
Issue. 09,
p.
959.
Zheng, Hao
2007.
Proof of the Volume Conjecture for Whitehead Doubles of a Family of Torus Knots.
Chinese Annals of Mathematics, Series B,
Vol. 28,
Issue. 4,
p.
375.
HIKAMI, KAZUHIRO
and
MURAKAMI, HITOSHI
2008.
COLORED JONES POLYNOMIALS WITH POLYNOMIAL GROWTH.
Communications in Contemporary Mathematics,
Vol. 10,
Issue. supp01,
p.
815.
TAKATA, TOSHIE
2009.
OHTSUKI INVARIANTS FOR INTEGRAL HOMOLOGY SPHERES AND HABIRO'S CYCLOTOMIC EXPANSION.
Journal of Knot Theory and Its Ramifications,
Vol. 18,
Issue. 01,
p.
21.
Dijkgraaf, Robbert
Fuji, Hiroyuki
and
Manabe, Masahide
2011.
The volume conjecture, perturbative knot invariants, and recursion relations for topological strings.
Nuclear Physics B,
Vol. 849,
Issue. 1,
p.
166.
Cherednik, Ivan
2013.
Jones Polynomials of Torus Knots via DAHA.
International Mathematics Research Notices,
Vol. 2013,
Issue. 23,
p.
5366.
Garoufalidis, Stavros
Morton, Hugh
and
Vuong, Thao
2013.
The 𝑆𝐿₃ colored Jones polynomial of the trefoil.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 6,
p.
2209.
Tran, Anh T
2013.
Proof of a stronger version of the AJ Conjecture for torus knots.
Algebraic & Geometric Topology,
Vol. 13,
Issue. 1,
p.
609.
Beem, Christopher
Dimofte, Tudor
and
Pasquetti, Sara
2014.
Holomorphic blocks in three dimensions.
Journal of High Energy Physics,
Vol. 2014,
Issue. 12,
Murakami, Hitoshi
2014.
The Colored Jones Polynomial, the Chern–Simons Invariant, and the Reidemeister Torsion of a Twice–Iterated Torus Knot.
Acta Mathematica Vietnamica,
Vol. 39,
Issue. 4,
p.
649.
Charles, L.
and
Marché, J.
2015.
Knot state asymptotics I: AJ conjecture and Abelian representations.
Publications mathématiques de l'IHÉS,
Vol. 121,
Issue. 1,
p.
279.
Ruppe, Dennis
and
Zhang, Xingru
2015.
The AJ-Conjecture and cabled knots over torus knots.
Journal of Knot Theory and Its Ramifications,
Vol. 24,
Issue. 09,
p.
1550051.

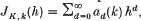 , where
, where 