Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T12:40:24.244Z Has data issue: false hasContentIssue false
  • English
  • Français

The Compton Effect in Wave Mechanics

Published online by Cambridge University Press:  24 October 2008

P. A. M. Dirac
P. A. M. Dirac
Affiliation:
St John's College
Get access Rights & Permissions [Opens in a new window]

Extract

The problem of the scattering of radiation by a free electron has been treated by the author on the basis of Heisenberg's matrix mechanics, which was first modified to be in agreement with the principle of relativity. The main point of this modification is that, whereas in the non-relativity theory one deals with matrices whose elements vary with the time according to the law eiwt, in the relativity theory the elements of the matrices must vary according to the law eiwt′ where t′ = t − (l1x1 + l2x2 + l3x3)/c if they are to determine correctly the radiation emitted in the direction specified by the direction cosines (l1, l2, l3), x1x2 and x3 being the coordinates of the electron at the time t. These matrices were obtained by writing the Hamiltonian equation of the system in the form

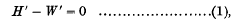
where W′ is a variable canonically conjugate to t′ and H′ commutes with t′, and then using H′ as an ordinary Hamiltonian function of a dynamical, system that has W′ for its energy and t′ for its time variable.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 5 , January 1927 , pp. 500 - 507
Copyright
Copyright © Cambridge Philosophical Society 1927

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Roy. Soc. Proc. A, vol. 111, p. 405 (1926). This paper is referred to later by loc. cit.CrossRefGoogle Scholar

† See Schrödinger's papers in the Ann. d. Phys., vols. 79–81 (1926)Google Scholar. For the general method of obtaining matrices from the wave mechanics, see section 2 of the author's paper, Roy. Soc. Proc. A, vol. 112, p. 661 (1926).CrossRefGoogle Scholar

* Loc. cit., equation (21).Google Scholar

* Loc. cit., equations (33).Google Scholar

* Note added in proof:—A paper by W. Gordon dealing with the same subject has recently appeared [Zeits. f. Phys., vol. 40, p. 117 (1926)]. Gordon's method makes use of an expression for the electric density for determining the field produced by the scattering electron, and differs from the method of the present paper, in which the wave equation is used merely as a mathematical help for the calculation of the matrix elements, which are then interpreted in accordance with the assumptions of matrix mechanics.CrossRefGoogle Scholar