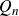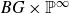1. Introduction
Let p be a prime number and
![]() $A={\mathbb Q},{\mathbb Z}$
or
$A={\mathbb Q},{\mathbb Z}$
or
![]() ${\mathbb Z}/p^i$
for
${\mathbb Z}/p^i$
for
![]() $i\ge 1$
. Let X be a smooth algebraic variety over
$i\ge 1$
. Let X be a smooth algebraic variety over
![]() $k={\mathbb C}$
. Let us recall the coniveau filtration of the cohomology with coefficients in A,
$k={\mathbb C}$
. Let us recall the coniveau filtration of the cohomology with coefficients in A,
where
![]() $Z\subset X$
runs through the closed subvarieties of codimension at least c of X, and
$Z\subset X$
runs through the closed subvarieties of codimension at least c of X, and
![]() $j\,:\,X-Z\subset X$
is the complementary open immersion.
$j\,:\,X-Z\subset X$
is the complementary open immersion.
Similarly, we can define the strong coniveau filtration by
where the sum is over all proper morphism
![]() $f\,:\, Y\to X$
from a smooth complex variety Y of
$f\,:\, Y\to X$
from a smooth complex variety Y of
![]() $dim(Y)=dim(X)-r$
with
$dim(Y)=dim(X)-r$
with
![]() $r\ge c$
, and
$r\ge c$
, and
![]() $f_*$
its transfer (Gysin map). It is immediate that
$f_*$
its transfer (Gysin map). It is immediate that
![]() $\tilde N^cH^*(X;\,A)\subset N^cH^*(X;\,A)$
.
$\tilde N^cH^*(X;\,A)\subset N^cH^*(X;\,A)$
.
It was hoped that when X is proper, the strong coniveau filtration was just the coniveau filtration, i.e.,
![]() $ \tilde N^cH^i(X;\,A)=N^cH^i(X;\,A)$
. In fact Deligne shows that they are the same for
$ \tilde N^cH^i(X;\,A)=N^cH^i(X;\,A)$
. In fact Deligne shows that they are the same for
![]() $A={\mathbb Q}$
. However, Benoist and Ottem ([
Reference Benoist and Ottem1
]) recently show that they are not equal for
$A={\mathbb Q}$
. However, Benoist and Ottem ([
Reference Benoist and Ottem1
]) recently show that they are not equal for
![]() $A={\mathbb Z}$
.
$A={\mathbb Z}$
.
Let G be an algebraic group such that
![]() $H^*(BG;\,{\mathbb Z})$
has p-torsion for the (geometric) classifying space BG defined by Totaro [
Reference Totaro17
] as a colimit of smooth quasi-projective varieties. Moreover, Ekedahl [
Reference Ekedahl4
] shows that
$H^*(BG;\,{\mathbb Z})$
has p-torsion for the (geometric) classifying space BG defined by Totaro [
Reference Totaro17
] as a colimit of smooth quasi-projective varieties. Moreover, Ekedahl [
Reference Ekedahl4
] shows that
![]() $BG\times {\mathbb P}^{\infty} $
can be approximated by smooth projective varieties X in the following sense.
$BG\times {\mathbb P}^{\infty} $
can be approximated by smooth projective varieties X in the following sense.
Here a (degree N) approximation is the projective smooth variety
![]() $X=X(N)$
such that there is a map
$X=X(N)$
such that there is a map
![]() $g\,:\,X\to BG\times {\mathbb P}^{\infty}$
with
$g\,:\,X\to BG\times {\mathbb P}^{\infty}$
with
The aim of this paper is to compute the mod(p) stable birational invariant of X [ Reference Benoist and Ottem1 , proposition 2·4]
for projective approximations X of
![]() $BG\times {\mathbb P}^{\infty}$
([
Reference Ekedahl4
,
Reference Pirutka and Yagita10
]). In fact, we see that
$BG\times {\mathbb P}^{\infty}$
([
Reference Ekedahl4
,
Reference Pirutka and Yagita10
]). In fact, we see that
![]() $DH^*(X;\,{\mathbb Z})\not =0$
happen very frequently in the above cases. In this paper, we say that X is an approximation for BG when it is that of
$DH^*(X;\,{\mathbb Z})\not =0$
happen very frequently in the above cases. In this paper, we say that X is an approximation for BG when it is that of
![]() $BG\times {\mathbb P}^{\infty} $
strictly speaking. Let us write
$BG\times {\mathbb P}^{\infty} $
strictly speaking. Let us write
![]() $DH^*(X;\,{\mathbb Z})$
by
$DH^*(X;\,{\mathbb Z})$
by
![]() $DH^*(X)$
simply as usual.
$DH^*(X)$
simply as usual.
Here we give an example that we can compute a nonzero
![]() $DH^*(X)$
. For
$DH^*(X)$
. For
![]() $G=({\mathbb Z}/p)^3$
the elementary abelian p-group of
$G=({\mathbb Z}/p)^3$
the elementary abelian p-group of
![]() $rank=3$
, we know (for p odd)
$rank=3$
, we know (for p odd)
where
![]() $Q_0=\beta$
is the Bockstein operation,
$Q_0=\beta$
is the Bockstein operation,
![]() $\Lambda(a,...,b)$
is the
$\Lambda(a,...,b)$
is the
![]() ${\mathbb Z}/p$
-exterior algebra generated by
${\mathbb Z}/p$
-exterior algebra generated by
![]() $a,...,b$
. and the notation
$a,...,b$
. and the notation
![]() $R(a,...,b)$
(resp.
$R(a,...,b)$
(resp.
![]() $R\{a,..., b\}$
) means the R-submodule (resp. the free R-module) generated by
$R\{a,..., b\}$
) means the R-submodule (resp. the free R-module) generated by
![]() $a,...,b$
.
$a,...,b$
.
Theorem 1·1.
Let
![]() $G=({\mathbb Z}/p)^3$
. For all
$G=({\mathbb Z}/p)^3$
. For all
![]() $N>2p+3$
and all (degree N) approximations
$N>2p+3$
and all (degree N) approximations
![]() $X=X(N)$
for BG, we have
$X=X(N)$
for BG, we have
But we have
![]() $DH^*(X;\,{\mathbb Z}/p)=0$
for all degree
$DH^*(X;\,{\mathbb Z}/p)=0$
for all degree
![]() $*<N$
.
$*<N$
.
Remark. In general,
![]() $DH^*(X)$
seems not to be an invariant of BG, but the above case is determined by BG. Many cases of examples in this paper have this property.
$DH^*(X)$
seems not to be an invariant of BG, but the above case is determined by BG. Many cases of examples in this paper have this property.
Benoist and Ottem also study approximations of
![]() $BG\times {\mathbb P}^{\infty}$
. They compute for example
$BG\times {\mathbb P}^{\infty}$
. They compute for example
![]() $G=({\mathbb Z}/2)^3$
and show that the invariant is nonzero for
$G=({\mathbb Z}/2)^3$
and show that the invariant is nonzero for
![]() $A={\mathbb Z}_{(2)}$
by using compositions of the Steenrod squares and Wu theorems. On the other hand, we show that arguments can be extended for
$A={\mathbb Z}_{(2)}$
by using compositions of the Steenrod squares and Wu theorems. On the other hand, we show that arguments can be extended for
![]() $A={\mathbb Z}_{(p)}$
for all prims p by using the Milnor operation
$A={\mathbb Z}_{(p)}$
for all prims p by using the Milnor operation
![]() $Q_n$
, which commutes with all Gysin maps.
$Q_n$
, which commutes with all Gysin maps.
However it seems not so easy to give a nontrivial example for
![]() $A={\mathbb Z}/p$
in the case X is an approximation for BG as the above examples show.
$A={\mathbb Z}/p$
in the case X is an approximation for BG as the above examples show.
For connected groups we have
Theorem 1·2.
Let G be a simply connected group such that
![]() $H^*(BG)$
has p-torsion. Let
$H^*(BG)$
has p-torsion. Let
![]() $N>2p+3$
. Then all degree N approximation X for BG, we have
$N>2p+3$
. Then all degree N approximation X for BG, we have
![]() $ DH^4(X)\not =0.$
$ DH^4(X)\not =0.$
Theorem 1·3.
Let p be an odd prime number, and
![]() $G=PGL_p$
. Let
$G=PGL_p$
. Let
![]() $N>2p+2$
. Then for all degree N approximation X for BG, we have
$N>2p+2$
. Then for all degree N approximation X for BG, we have
![]() $DH^3(X)\not =0$
.
$DH^3(X)\not =0$
.
Theorem 1·4.
Let
![]() $p=2$
and
$p=2$
and
![]() $X_{2m+1}=X_{2m+1}(N)$
be an approximation for
$X_{2m+1}=X_{2m+1}(N)$
be an approximation for
![]() $BSO_{2m+1}$
of degree
$BSO_{2m+1}$
of degree
![]() $N\ge 3$
. Then there exists
$N\ge 3$
. Then there exists
![]() $0<L=L(m)$
such that for all approximations
$0<L=L(m)$
such that for all approximations
![]() $X_{2m+1}$
of degree
$X_{2m+1}$
of degree
![]() $N>L$
, we have
$N>L$
, we have
where
![]() $w_i$
is the ith Stiefel–Whiteny class for
$w_i$
is the ith Stiefel–Whiteny class for
![]() $SO_{2m+1}\subset O_{2m+1}$
.
$SO_{2m+1}\subset O_{2m+1}$
.
2. Transfer and
 $Q_n$
$Q_n$
The Milnor operation (in
![]() $H^*({-};\,{\mathbb Z}/p)$
) is defined by
$H^*({-};\,{\mathbb Z}/p)$
) is defined by
![]() $Q_0=\beta$
and for
$Q_0=\beta$
and for
![]() $n\ge 1$
$n\ge 1$
(for details see [
Reference Milnor8
], [
Reference Voevodsky18
, section 3·1]), where
![]() $\beta$
is the Bockstein operation and
$\beta$
is the Bockstein operation and
![]() $P^{\alpha}$
for
$P^{\alpha}$
for
![]() $\alpha=(\alpha_1,\alpha_2,...)$
is the fundamental base of the module of finite sums of products of reduced powers.
$\alpha=(\alpha_1,\alpha_2,...)$
is the fundamental base of the module of finite sums of products of reduced powers.
Lemma 2·1.
Let
![]() $f_*$
be the transfer (Gysin) map (for proper smooth)
$f_*$
be the transfer (Gysin) map (for proper smooth)
![]() $f\,:\,X\to Y$
. Then
$f\,:\,X\to Y$
. Then
![]() $Q_nf_*(x)=f_*Q_n(x)$
for
$Q_nf_*(x)=f_*Q_n(x)$
for
![]() $x\in H^*(X;\,{\mathbb Z}/p)$
.
$x\in H^*(X;\,{\mathbb Z}/p)$
.
The above lemma is known (see the proof of [
Reference Yagita23
, lemma 7·1]). The transfer
![]() $f_*$
is expressed as
$f_*$
is expressed as
![]() $g^*f^{\prime}_*$
such that
$g^*f^{\prime}_*$
such that
for some maps g, f
′, i and the Thom class Th(1). Since
![]() $Q_n(Th(1))=0$
and
$Q_n(Th(1))=0$
and
![]() $Q_n$
is a derivation, we get the lemma. However, we give here the another computational proof.
$Q_n$
is a derivation, we get the lemma. However, we give here the another computational proof.
Proof of Lemma 2·1. Recall the following Grothendieck formula (e.g., [Q1])
Here the total reduced powers
![]() $P_t(x)$
are defined
$P_t(x)$
are defined
where
![]() $\alpha=(\alpha_1,\alpha_2,...)$
and
$\alpha=(\alpha_1,\alpha_2,...)$
and
![]() $degree(t^{\alpha})=\sum_i 2\alpha_i\left(p^i-1\right)$
(each element in the cohomology
$degree(t^{\alpha})=\sum_i 2\alpha_i\left(p^i-1\right)$
(each element in the cohomology
![]() $H^*(X;\,{\mathbb Z}/p)$
is represented as a homogeneous part respective to the above degree). The total Chern class
$H^*(X;\,{\mathbb Z}/p)$
is represented as a homogeneous part respective to the above degree). The total Chern class
![]() $c_t$
is defined similarly, for the Chern classes of the normal bundle of the map f.
$c_t$
is defined similarly, for the Chern classes of the normal bundle of the map f.
We consider the above equation with the assumption such that
![]() $t_n^2=0$
and
$t_n^2=0$
and
![]() $t_j=0$
for
$t_j=0$
for
![]() $j\not =n$
, i.e.,
$j\not =n$
, i.e.,
![]() $P_t(x)\in H^*(X;\,{\mathbb Z}/p)\otimes \Lambda(t_n)$
. That means
$P_t(x)\in H^*(X;\,{\mathbb Z}/p)\otimes \Lambda(t_n)$
. That means
 \begin{align} f_*\left(c_t\cdot P_t(x)\right) & =f_*\left(\left(1+c_{p^n-1}t_n\right)\left(x+P^{\Delta_n}(x)t_n\right)\right)\nonumber\\& =f_*\left(x+\left(c_{p^n-1}x+P^{\Delta_n}(x)\right)t_n\right).\end{align}
\begin{align} f_*\left(c_t\cdot P_t(x)\right) & =f_*\left(\left(1+c_{p^n-1}t_n\right)\left(x+P^{\Delta_n}(x)t_n\right)\right)\nonumber\\& =f_*\left(x+\left(c_{p^n-1}x+P^{\Delta_n}(x)\right)t_n\right).\end{align}
From (1), we see
![]() $(2)=(3)$
and we have
$(2)=(3)$
and we have
By the definition,
![]() $\beta$
commutes with
$\beta$
commutes with
![]() $f_*$
, and we have
$f_*$
, and we have
On the other hand
Then (5)–(6) gives that
![]() $\left(P^{\Delta_n} \beta-\beta P^{\Delta_n}\right)f_*(x)=f_*\left(P^{\Delta_n} \beta-\beta P^{\Delta_n}\right)(x).$
Thus we can prove Lemma 2·1.
$\left(P^{\Delta_n} \beta-\beta P^{\Delta_n}\right)f_*(x)=f_*\left(P^{\Delta_n} \beta-\beta P^{\Delta_n}\right)(x).$
Thus we can prove Lemma 2·1.
By the definition, each cohomology operation h (i.e., an element in the Steenrod algebra) is written
![]() $\big($
with
$\big($
with
![]() $Q^B=Q_0^{b_0}Q_1^{b_1}...\big)$
by
$Q^B=Q_0^{b_0}Q_1^{b_1}...\big)$
by
Corollary 2·2.
We have
![]() $ P_tQ^B\left(f_*(x)\right)=f_*\left(c_t\cdot P_tQ^B(x)\right).$
$ P_tQ^B\left(f_*(x)\right)=f_*\left(c_t\cdot P_tQ^B(x)\right).$
Hence cohomology operations h (for
![]() $H^*({-};\,{\mathbb Z}/p))$
which commute with all transfer
$H^*({-};\,{\mathbb Z}/p))$
which commute with all transfer
![]() $f_*$
are cases
$f_*$
are cases
![]() $c_t=1$
, i.e.
$c_t=1$
, i.e.
![]() $A=0$
which are only products
$A=0$
which are only products
![]() $Q^B$
of Milnor operations
$Q^B$
of Milnor operations
![]() $Q_i$
.
$Q_i$
.
3. Coniveau filtrations
Bloch–Ogus [
Reference Bloch and Ogus2
] give a spectral sequence such that its
![]() $E_2$
-term is given by
$E_2$
-term is given by
where
![]() $\mathcal{H}_{A}^*$
is the Zariski sheaf induced from the presheaf given by
$\mathcal{H}_{A}^*$
is the Zariski sheaf induced from the presheaf given by
![]() $U\mapsto H_{et}^*(U;\,A)$
for an open
$U\mapsto H_{et}^*(U;\,A)$
for an open
![]() $U\subset X$
.
$U\subset X$
.
The filtration for this spectral sequence is defined as the coniveau filtration
where the infinite term
![]() $ E(c)^{c,*-c}_{\infty}\cong F(c)^{c,*-c}/F(c)^{c+1,*-c-1}$
and
$ E(c)^{c,*-c}_{\infty}\cong F(c)^{c,*-c}/F(c)^{c+1,*-c-1}$
and
Here we recall the motivic cohomology
![]() $H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$
defined by Voevodsky and Suslin ([
Reference Voevodsky18
,
Reference Voevodsky20
,
Reference Voevodsky21
]) so that
$H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$
defined by Voevodsky and Suslin ([
Reference Voevodsky18
,
Reference Voevodsky20
,
Reference Voevodsky21
]) so that
Let us write
![]() $H^*_{et}(X;\,{\mathbb Z} )$
simply by
$H^*_{et}(X;\,{\mathbb Z} )$
simply by
![]() $H^*_{et}(X)$
as usual. Note that
$H^*_{et}(X)$
as usual. Note that
![]() $H^*_{et}(X)\not \cong H^*(X)$
in general, while we have the natural map
$H^*_{et}(X)\not \cong H^*(X)$
in general, while we have the natural map
![]() $H_{et}^*(X)\to H^*(X)$
.
$H_{et}^*(X)\to H^*(X)$
.
Let
![]() $0\not =\tau \in H^{0,1}(Spec({\mathbb C});\,{\mathbb Z}/p)$
. Then by the multiplying
$0\not =\tau \in H^{0,1}(Spec({\mathbb C});\,{\mathbb Z}/p)$
. Then by the multiplying
![]() $\tau$
, we can define a map
$\tau$
, we can define a map
![]() $H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)\to H^{*,*^{\prime}+1}(X;\,{\mathbb Z}/p)$
. By Deligne ([
Reference Bloch and Ogus2
, foot note (1) in Remark 6·4]) and Paranjape ([
Reference Paranjape9
, corollary 4·4]), it is proven that there is an isomorphism of the coniveau spectral sequence with the
$H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)\to H^{*,*^{\prime}+1}(X;\,{\mathbb Z}/p)$
. By Deligne ([
Reference Bloch and Ogus2
, foot note (1) in Remark 6·4]) and Paranjape ([
Reference Paranjape9
, corollary 4·4]), it is proven that there is an isomorphism of the coniveau spectral sequence with the
![]() $\tau$
-Bockstein spectral sequence
$\tau$
-Bockstein spectral sequence
![]() $E(\tau)_r^{*,*^{\prime}}$
(see also [
Reference Tezuka and Yagita16
,
Reference Yagita22
]).
$E(\tau)_r^{*,*^{\prime}}$
(see also [
Reference Tezuka and Yagita16
,
Reference Yagita22
]).
Lemma 3·1.
(Deligne) Let
![]() $A={\mathbb Z}/p$
. Then we have the isomorphism of spectral sequence
$A={\mathbb Z}/p$
. Then we have the isomorphism of spectral sequence
Hence the filtrations are the same, i.e.
![]() $N^cH_{et}^*(X;\,{\mathbb Z}/p)= F_{\tau}^{*,*-c}$
where
$N^cH_{et}^*(X;\,{\mathbb Z}/p)= F_{\tau}^{*,*-c}$
where
Lemma 3·2.
Suppose that
![]() $x\in H^{*,*}(X)$
and for
$x\in H^{*,*}(X)$
and for
![]() $c>0$
its mod(p) reduction
$c>0$
its mod(p) reduction
![]() $r(x)\in N^cH^*(X;\,{\mathbb Z}/p)$
. Then if the map
$r(x)\in N^cH^*(X;\,{\mathbb Z}/p)$
. Then if the map
![]() $f\,:\,H^{*+1,*-c}(X)\to H^{*+1,*}(X)$
is injective, then
$f\,:\,H^{*+1,*-c}(X)\to H^{*+1,*}(X)$
is injective, then
![]() $x\in N^cH^*(X)$
mod(p).
$x\in N^cH^*(X)$
mod(p).
Proof. Consider the exact sequences

.
By the assumption of this lemma, we can take
![]() $x^{\prime}\in H^{*,*-c}(X;\,{\mathbb Z}/p)$
such that
$x^{\prime}\in H^{*,*-c}(X;\,{\mathbb Z}/p)$
such that
![]() $r_2(x)=f_2(x^{\prime})$
. So
$r_2(x)=f_2(x^{\prime})$
. So
![]() $\delta_2f_2(x^{\prime})=0$
. Since
$\delta_2f_2(x^{\prime})=0$
. Since
![]() $f_3$
is injective, we see
$f_3$
is injective, we see
![]() $\delta_1(x^{\prime})=0$
, Hence there is
$\delta_1(x^{\prime})=0$
, Hence there is
![]() $x^{\prime\prime}\in H^{*.*-c^{\prime}}(X)$
such that
$x^{\prime\prime}\in H^{*.*-c^{\prime}}(X)$
such that
![]() $r_1(x^{\prime\prime})=x^{\prime}$
. Thus we have the lemma.
$r_1(x^{\prime\prime})=x^{\prime}$
. Thus we have the lemma.
Let
![]() $cl\,:\, CH^*(X)\otimes A\to H^{2*}(X;\,A)$
be the cycle map, and
$cl\,:\, CH^*(X)\otimes A\to H^{2*}(X;\,A)$
be the cycle map, and
![]() $Im(cl)^+$
be the positive degree parts of its image.
$Im(cl)^+$
be the positive degree parts of its image.
Lemma 3·3.
We see that
![]() $Im(cl)^+\subset N^*H^{2*}(X;\,A)$
.
$Im(cl)^+\subset N^*H^{2*}(X;\,A)$
.
Proof. Recall that
![]() $H^{*.*^{\prime}}(X;\,A)\to N^{*-*^{\prime}}H^*(X;\,A)$
. We have
$H^{*.*^{\prime}}(X;\,A)\to N^{*-*^{\prime}}H^*(X;\,A)$
. We have
![]() $H^{2*,*}(X;\,A)\cong CH^*(X)\otimes A.$
Since
$H^{2*,*}(X;\,A)\cong CH^*(X)\otimes A.$
Since
![]() $2*>*$
for
$2*>*$
for
![]() $*\ge 1$
, we see
$*\ge 1$
, we see
![]() $cl(y)\in N^{1}H^{2*}(X;\,A)$
.
$cl(y)\in N^{1}H^{2*}(X;\,A)$
.
Each element
![]() $y\in CH^*(X)\otimes A$
is represented by closed algebraic set supported Y, while Y may be singular. On the other hand, by Totaro [
Reference Totaro17
], we have the modified cycle map
$y\in CH^*(X)\otimes A$
is represented by closed algebraic set supported Y, while Y may be singular. On the other hand, by Totaro [
Reference Totaro17
], we have the modified cycle map
![]() $\bar cl$
$\bar cl$
for the complex cobordism theory
![]() $MU^*(X)$
. It is known [
Reference Quillen11
] that elements in
$MU^*(X)$
. It is known [
Reference Quillen11
] that elements in
![]() $MU^{2*}(X)$
can be represented by proper maps to X from stable almost complex manifolds Y. (The manifold Y is not necessarily a complex manifold.)
$MU^{2*}(X)$
can be represented by proper maps to X from stable almost complex manifolds Y. (The manifold Y is not necessarily a complex manifold.)
The following lemma is well known.
Lemma 3·4.
If
![]() $x\in Im(\rho)$
for
$x\in Im(\rho)$
for
![]() $\rho\,:\, MU^*(X)/p\to H^*(X;\,{\mathbb Z}/p)$
, then we have
$\rho\,:\, MU^*(X)/p\to H^*(X;\,{\mathbb Z}/p)$
, then we have
![]() $Q_i(x)=0$
for all
$Q_i(x)=0$
for all
![]() $i\ge 0$
.
$i\ge 0$
.
Proof. Recall the connective Morava K-theory
![]() $k(i)^*(X)$
with
$k(i)^*(X)$
with
![]() $k(i)^*={\mathbb Z}/p[v_i]$
,
$k(i)^*={\mathbb Z}/p[v_i]$
,
![]() $|v_i|=-2p^i+2$
, which has natural maps
$|v_i|=-2p^i+2$
, which has natural maps
It is known that
![]() $d_{2p^i-1}=Q_i$
for the first nonzero differential
$d_{2p^i-1}=Q_i$
for the first nonzero differential
![]() $d_{2p^i-1}$
of the Atiyah-Hirzebruch spectral sequence converging to
$d_{2p^i-1}$
of the Atiyah-Hirzebruch spectral sequence converging to
![]() $k(i)^*(X)$
,
$k(i)^*(X)$
,
Hence
![]() $Q_i\rho_2(x)=0$
which implies
$Q_i\rho_2(x)=0$
which implies
![]() $Q_i\rho(x)=0$
.
$Q_i\rho(x)=0$
.
Lemma 3·5.
(reciprocity law) If
![]() $a\in \tilde N^1H^{*}(X;\,A)$
, then for each
$a\in \tilde N^1H^{*}(X;\,A)$
, then for each
![]() $g\in H^{*^{\prime}}(X;\,A)$
we have
$g\in H^{*^{\prime}}(X;\,A)$
we have
![]() $ag\in \tilde N^1H^{*+*^{\prime}}(X;\,A)$
.
$ag\in \tilde N^1H^{*+*^{\prime}}(X;\,A)$
.
Proof. Suppose we have
![]() $f\,:\,Y\to X$
with
$f\,:\,Y\to X$
with
![]() $f_*(a^{\prime})=a$
. Then
$f_*(a^{\prime})=a$
. Then
by Frobenius reciprocity law.
Let G be an algebraic group (over
![]() ${\mathbb C}$
) and r be a complex representation
${\mathbb C}$
) and r be a complex representation
![]() $r\,:\,G\to U_n$
for the unitary group
$r\,:\,G\to U_n$
for the unitary group
![]() $U_n$
. Then we can define the Chern class
$U_n$
. Then we can define the Chern class
![]() $c_i=r^*c_i^U$
. Here the Chern classes
$c_i=r^*c_i^U$
. Here the Chern classes
![]() $c_i^U$
in
$c_i^U$
in
![]() $H^*(BU_n)\cong {\mathbb Z}\!\left[c_1^U,...,c_n^U\right]$
are defined by the Gysin map
$H^*(BU_n)\cong {\mathbb Z}\!\left[c_1^U,...,c_n^U\right]$
are defined by the Gysin map
![]() $c_n^U=i_{n*}(1)$
for the inclusion
$c_n^U=i_{n*}(1)$
for the inclusion
![]() $i_n\,:\,\{0\}\subset {\mathbb C}^{\times n}$
, that is,
$i_n\,:\,\{0\}\subset {\mathbb C}^{\times n}$
, that is,
where
![]() $H_{U_n}({-})=H^*(EU_n\times_{U_n}-)$
is the
$H_{U_n}({-})=H^*(EU_n\times_{U_n}-)$
is the
![]() $U_n$
-equivariant cohomology. Hence for the approximation
$U_n$
-equivariant cohomology. Hence for the approximation
![]() $XU_n$
for
$XU_n$
for
![]() $U_n$
, we see
$U_n$
, we see
![]() $c_i^{U}\in \tilde N^1H^*(XU_n)$
. So
$c_i^{U}\in \tilde N^1H^*(XU_n)$
. So
![]() $c_i=r^*c_i^U\in\tilde N ^{1}H^*(X)$
for the approximation X for BG.
$c_i=r^*c_i^U\in\tilde N ^{1}H^*(X)$
for the approximation X for BG.
By the reciprocity law (Lemma 3·5) we have
Lemma 3·6.
Let
![]() $c_i=r^*c_i^U\in H^*(BG)$
be a Chern class for some representation
$c_i=r^*c_i^U\in H^*(BG)$
be a Chern class for some representation
![]() $r\,:\, G\to U_n$
. For an approximation X for BG and for each
$r\,:\, G\to U_n$
. For an approximation X for BG and for each
![]() $g\in H^{*^{\prime}}(BG)$
, we have
$g\in H^{*^{\prime}}(BG)$
, we have
![]() $gc_i\in \tilde N^1H^*(X)$
.
$gc_i\in \tilde N^1H^*(X)$
.
The following lemma is proved by Colliot Thérène and Voisin [ Reference Colliot Thérène and Voisin3 ] by using the affirmative answer of the Bloch–Kato conjecture by Voevodsky ([ Reference Voevodsky20 , Reference Voevodsky21 ]).
Lemma 3·7. ([
Reference Colliot Thérène and Voisin3
]) Let X be a smooth complex variety. Then any torsion element in
![]() $H^*(X)$
is in
$H^*(X)$
is in
![]() $N^1H^*(X)$
.
$N^1H^*(X)$
.
4. The main lemmas
The following lemma is the
![]() $Q_i$
-version of one of results by Benoist and Ottem.
$Q_i$
-version of one of results by Benoist and Ottem.
Lemma 4·1.
Let
![]() $\alpha\in N^1H^s(X)$
for
$\alpha\in N^1H^s(X)$
for
![]() $s=3$
or 4. If
$s=3$
or 4. If
![]() $Q_i(\alpha)\not =0\in H^*(X;\,{\mathbb Z}/p)$
for some
$Q_i(\alpha)\not =0\in H^*(X;\,{\mathbb Z}/p)$
for some
![]() $i\ge 1$
, then
$i\ge 1$
, then
Proof. Suppose
![]() $\alpha\in \tilde N^1H^s(X)$
for
$\alpha\in \tilde N^1H^s(X)$
for
![]() $s=3$
or 4, i.e. there is a smooth Y with
$s=3$
or 4, i.e. there is a smooth Y with
![]() $f\,:\,Y\to X$
such that the transfer
$f\,:\,Y\to X$
such that the transfer
![]() $f_*\left(\alpha^{\prime}\right)=\alpha$
for
$f_*\left(\alpha^{\prime}\right)=\alpha$
for
![]() $\alpha^{\prime}\in H^*(Y)$
. Then for
$\alpha^{\prime}\in H^*(Y)$
. Then for
![]() $s=4$
$s=4$
 \begin{align*} Q_i\left(\alpha^{\prime}\right) & =\left(P^{\Delta_i}\beta-\beta P^{\Delta_i}\right)\left(\alpha^{\prime}\right)=\left({-}\beta P^{\Delta_i}\right)\left(\alpha^{\prime}\right) = -\beta \!\left(\alpha^{\prime}\right)^{p^i}\\[4pt]& =-p^i\left(\beta \alpha^{\prime}\right)\left(\alpha^{\prime}\right)^{p^i-1}=0 \quad (by\ Cartan\ formula)\end{align*}
\begin{align*} Q_i\left(\alpha^{\prime}\right) & =\left(P^{\Delta_i}\beta-\beta P^{\Delta_i}\right)\left(\alpha^{\prime}\right)=\left({-}\beta P^{\Delta_i}\right)\left(\alpha^{\prime}\right) = -\beta \!\left(\alpha^{\prime}\right)^{p^i}\\[4pt]& =-p^i\left(\beta \alpha^{\prime}\right)\left(\alpha^{\prime}\right)^{p^i-1}=0 \quad (by\ Cartan\ formula)\end{align*}
since
![]() $\beta\!\left(\alpha^{\prime}\right)=0$
and
$\beta\!\left(\alpha^{\prime}\right)=0$
and
![]() $P^{\Delta_i}(y)=y^{p^i}$
for
$P^{\Delta_i}(y)=y^{p^i}$
for
![]() $deg(y)=2$
. (For
$deg(y)=2$
. (For
![]() $s=3$
, we get also
$s=3$
, we get also
![]() $Q_i\left(\alpha^{\prime}\right)=0$
since
$Q_i\left(\alpha^{\prime}\right)=0$
since
![]() $ P^{\Delta_i}(x)=0$
for
$ P^{\Delta_i}(x)=0$
for
![]() $deg(x)=1$
.) This contradicts the commutativity of
$deg(x)=1$
.) This contradicts the commutativity of
![]() $Q_i$
and
$Q_i$
and
![]() $f_*$
.
$f_*$
.
The case
![]() $A={\mathbb Z}/p^t$
,
$A={\mathbb Z}/p^t$
,
![]() $t\ge 2$
is proved similarly, since for
$t\ge 2$
is proved similarly, since for
![]() $\alpha^{\prime}\in H^*(X;\,A)$
we see
$\alpha^{\prime}\in H^*(X;\,A)$
we see
![]() $\beta \alpha^{\prime}=0\in H^*(X;\,{\mathbb Z}/p)$
. Thus we have this lemma.
$\beta \alpha^{\prime}=0\in H^*(X;\,{\mathbb Z}/p)$
. Thus we have this lemma.
We will extend Lemma 4·1 to
![]() $s>4$
, by using MU-theory of Eilenberg–MacLane spaces. Recall that
$s>4$
, by using MU-theory of Eilenberg–MacLane spaces. Recall that
![]() $K=K({\mathbb Z},n)$
is the Eilenberg–MacLane space such that the homotopy group
$K=K({\mathbb Z},n)$
is the Eilenberg–MacLane space such that the homotopy group
![]() $[X,K]\cong H^n(X\,:\,{\mathbb Z})$
, i.e., each element
$[X,K]\cong H^n(X\,:\,{\mathbb Z})$
, i.e., each element
![]() $x\in H^n(X;\,{\mathbb Z})$
is represented by a homotopy map
$x\in H^n(X;\,{\mathbb Z})$
is represented by a homotopy map
![]() $x\,:\, X\to K$
. Let
$x\,:\, X\to K$
. Let
![]() $\eta_n\in H^n(K;\,{\mathbb Z})$
corresponding the identity map. (For
$\eta_n\in H^n(K;\,{\mathbb Z})$
corresponding the identity map. (For
![]() $K^{\prime}=K({\mathbb Z}/p,n)$
define
$K^{\prime}=K({\mathbb Z}/p,n)$
define
![]() $\eta^{\prime}_n\in H^n(K^{\prime};\,{\mathbb Z}/p)$
by the identity element of K
′.) We know the image
$\eta^{\prime}_n\in H^n(K^{\prime};\,{\mathbb Z}/p)$
by the identity element of K
′.) We know the image
![]() $\rho(MU^*(K))\subset H^*(K;\,{\mathbb Z})/p$
.
$\rho(MU^*(K))\subset H^*(K;\,{\mathbb Z})/p$
.
Lemma 4·2. ([ Reference Ravenel, Wilson and Yagita13 , Reference Tamanoi15 ]) We have the isomorphism
where the notation
![]() ${\mathbb Z}/p[a,...]$
exactly means
${\mathbb Z}/p[a,...]$
exactly means
![]() ${\mathbb Z}/p[a,...]/\left(a^2|\ |a|=odd\right)$
.
${\mathbb Z}/p[a,...]/\left(a^2|\ |a|=odd\right)$
.
The following lemma is an extension of Lemma 4·1 to
![]() $s> 4$
.
$s> 4$
.
Lemma 4·3.
Let
![]() $\alpha\in N^cH^{n+2c}(X)$
,
$\alpha\in N^cH^{n+2c}(X)$
,
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $c\ge 1$
. Suppose that there is a sequence
$c\ge 1$
. Suppose that there is a sequence
![]() $0<i_1< \cdots <i_{n-1}$
with
$0<i_1< \cdots <i_{n-1}$
with
Then
![]() $D^cH^{*}(X)=N^cH^{*}(X)/(p,\tilde N^cH^{*}(X)) \supset {\mathbb Z}/p\{\alpha\}$
.
$D^cH^{*}(X)=N^cH^{*}(X)/(p,\tilde N^cH^{*}(X)) \supset {\mathbb Z}/p\{\alpha\}$
.
Proof. Suppose
![]() $\alpha\in \tilde N^cH^{n+2c}(X)$
, i.e. there is a smooth Y of
$\alpha\in \tilde N^cH^{n+2c}(X)$
, i.e. there is a smooth Y of
![]() $dim(Y)=dim(X)-c$
with
$dim(Y)=dim(X)-c$
with
![]() $f\,:\,Y\to X$
such that the transfer
$f\,:\,Y\to X$
such that the transfer
![]() $f_*\left(\alpha^{\prime}\right)=\alpha$
for
$f_*\left(\alpha^{\prime}\right)=\alpha$
for
![]() $\alpha^{\prime}\in H^n(Y)$
.
$\alpha^{\prime}\in H^n(Y)$
.
Identify the map
![]() $\alpha^{\prime}\,:\, Y\to K$
with
$\alpha^{\prime}\,:\, Y\to K$
with
![]() $\alpha^{\prime}=\left(\alpha^{\prime}\right)^*\eta_n.$
We still see from Lemma 4·2,
$\alpha^{\prime}=\left(\alpha^{\prime}\right)^*\eta_n.$
We still see from Lemma 4·2,
From Lemma 3·4, we see
Therefore
![]() $Q_{i_{n-1}}Q(\alpha)$
must be zero by the commutativity of
$Q_{i_{n-1}}Q(\alpha)$
must be zero by the commutativity of
![]() $f_*$
and
$f_*$
and
![]() $Q_i$
.
$Q_i$
.
Remark. For
![]() $\alpha\in N^cH^{n+2c}(X;\,{\mathbb Z}/p)$
, one can prove an
$\alpha\in N^cH^{n+2c}(X;\,{\mathbb Z}/p)$
, one can prove an
![]() $A={\mathbb Z}/p$
version of the above lemma using the second isomorphism in Lemma 4·2. But we can see
$A={\mathbb Z}/p$
version of the above lemma using the second isomorphism in Lemma 4·2. But we can see
![]() $Q_{i_1}...Q_{i_n}Q_0\alpha=0$
always (even when
$Q_{i_1}...Q_{i_n}Q_0\alpha=0$
always (even when
![]() $Q_{i_1}...Q_{i_{n-1}}\alpha\not=0$
), hence
$Q_{i_1}...Q_{i_{n-1}}\alpha\not=0$
), hence
![]() ${\mathbb Z}/p$
version would be vacuous.
${\mathbb Z}/p$
version would be vacuous.
5. Classifying spaces for finite groups
Let G be a finite group or an algebraic group, and BG its (geometric) classifying space. For example, when
![]() $G=G_m$
is the multiplicative group, we see
$G=G_m$
is the multiplicative group, we see
for the infinite (complex) projective space
![]() ${\mathbb P}^{\infty}$
. Note that
${\mathbb P}^{\infty}$
. Note that
![]() $BG_m$
is a colimit of complex projective spaces.
$BG_m$
is a colimit of complex projective spaces.
Though BG itself is not a colimit of complex projective varieties, we can take a complex projective variety X(N) ([
Reference Ekedahl4
]) for a given
![]() $N\ge 3$
such that there is a map
$N\ge 3$
such that there is a map
![]() $ j\,:\,X(N)\to BG\times {\mathbb P}^{\infty} $
with
$ j\,:\,X(N)\to BG\times {\mathbb P}^{\infty} $
with
In this paper, we call the above X(N) a (degree
![]() $\ N$
) complex projective approximation for BG (which is an approximation of
$\ N$
) complex projective approximation for BG (which is an approximation of
![]() $BG\times {\mathbb P}^{\infty}$
strictly speaking).
$BG\times {\mathbb P}^{\infty}$
strictly speaking).
Note that the quotient
is an invariant under replacing X with
![]() $X\times {\mathbb P}^m$
for all n and all abelian groups A. In fact, from K
$X\times {\mathbb P}^m$
for all n and all abelian groups A. In fact, from K
![]() $\ddot{{u}}$
nneth formula,
$\ddot{{u}}$
nneth formula,
where
![]() $y\in CH^1({\mathbb P}^m)$
is the first Chern class. Let Ideal(y) be the ideal of
$y\in CH^1({\mathbb P}^m)$
is the first Chern class. Let Ideal(y) be the ideal of
![]() $H^*(X\times {\mathbb P}^m;\,A)$
generated by y. Then
$H^*(X\times {\mathbb P}^m;\,A)$
generated by y. Then
![]() $Ideal(y)\subset \tilde N^*H^*(X\times {\mathbb P}^{m};\,A)$
by the Frobenius reciprocity law (Lemma 3·5). Moreover Benoist and Ottem show that the above quotient when
$Ideal(y)\subset \tilde N^*H^*(X\times {\mathbb P}^{m};\,A)$
by the Frobenius reciprocity law (Lemma 3·5). Moreover Benoist and Ottem show that the above quotient when
![]() $n=1$
is a stable birational invariant of X ([
Reference Benoist and Ottem1
, proposition 2·4]).
$n=1$
is a stable birational invariant of X ([
Reference Benoist and Ottem1
, proposition 2·4]).
In this paper, we will study the following (mod(p)) stable rational invariant
Hereafter, we consider
![]() $DH^*(X;\,A)$
when
$DH^*(X;\,A)$
when
![]() $A={\mathbb Z}$
. Let p be an odd prime. (The case
$A={\mathbb Z}$
. Let p be an odd prime. (The case
![]() $p=2$
is different but a similar argument works.) Let
$p=2$
is different but a similar argument works.) Let
![]() $G=({\mathbb Z}/p)^3$
the
$G=({\mathbb Z}/p)^3$
the
![]() $rank=3$
elementary abelian p-group. Then the mod(p) cohomology is
$rank=3$
elementary abelian p-group. Then the mod(p) cohomology is
Here degree
![]() $|y_i|=2, |x_i|=1, \beta(x_i)=y_i$
, and
$|y_i|=2, |x_i|=1, \beta(x_i)=y_i$
, and
![]() $\Lambda(a,...,b)$
is the
$\Lambda(a,...,b)$
is the
![]() ${\mathbb Z}/p$
-exterior algebra generated by
${\mathbb Z}/p$
-exterior algebra generated by
![]() $a,...,b$
.
$a,...,b$
.
The integral cohomology (modulo p) is isomorphic to
where
![]() $H({-};\,Q_0)=Ker(Q_0)/Im(Q_0)$
is the homology with the differential
$H({-};\,Q_0)=Ker(Q_0)/Im(Q_0)$
is the homology with the differential
![]() $Q_0$
. It is immediate that
$Q_0$
. It is immediate that
![]() $H(H^*(B{\mathbb Z}/p;\,{\mathbb Z}/p);\, Q_0)\cong {\mathbb Z}/p$
. By the K
$H(H^*(B{\mathbb Z}/p;\,{\mathbb Z}/p);\, Q_0)\cong {\mathbb Z}/p$
. By the K
![]() $\ddot{u}$
nneth formula, we have
$\ddot{u}$
nneth formula, we have
![]() $H(H^*((BG;\,{\mathbb Z}/p);\,Q_0)\cong ( {\mathbb Z}/p)^{3\otimes}\cong {\mathbb Z}/p$
. Hence we have
$H(H^*((BG;\,{\mathbb Z}/p);\,Q_0)\cong ( {\mathbb Z}/p)^{3\otimes}\cong {\mathbb Z}/p$
. Hence we have
where the notation
![]() $R(a,...,b)$
(resp.
$R(a,...,b)$
(resp.
![]() $R\{a,..., b\}$
) means the R-submodule (resp. the free R-module) generated by
$R\{a,..., b\}$
) means the R-submodule (resp. the free R-module) generated by
![]() $a,...,b$
. Here we note
$a,...,b$
. Here we note
![]() $H^+(BG)$
is just p-torsion.
$H^+(BG)$
is just p-torsion.
Also note that
![]() $y_1,y_2,y_3$
are represented by the Chern classes
$y_1,y_2,y_3$
are represented by the Chern classes
![]() $c_1$
. From Lemma 3·6, we see
$c_1$
. From Lemma 3·6, we see
We know
![]() $Q_i(y_j)=y_j^{p^i}$
and
$Q_i(y_j)=y_j^{p^i}$
and
![]() $Q_j$
is a derivation. Let us write
$Q_j$
is a derivation. Let us write
Note
![]() $\alpha\in H^4(X)$
,
$\alpha\in H^4(X)$
,
![]() $p\alpha=0$
, and
$p\alpha=0$
, and
![]() $\alpha\in N^1H^*(X)$
from Lemma 3·7. Moreover
$\alpha\in N^1H^*(X)$
from Lemma 3·7. Moreover
Similarly, for
![]() $\alpha_{ij}=Q_0(x_ix_{j})$
, we see
$\alpha_{ij}=Q_0(x_ix_{j})$
, we see
![]() $Q_1(\alpha_{ij})\not =0$
. Hence from Lemma 4·1 and Lemma 3·6, we have
$Q_1(\alpha_{ij})\not =0$
. Hence from Lemma 4·1 and Lemma 3·6, we have
Theorem 5·1.
Let
![]() $X=X(N)$
with
$X=X(N)$
with
![]() $N> 2p+3$
be a (degree N) approximation for
$N> 2p+3$
be a (degree N) approximation for
![]() $B({\mathbb Z}/p)^3$
. Then we have
$B({\mathbb Z}/p)^3$
. Then we have
Proof. We see
![]() $H^*(BG)/(p,y_1,y_2,y_3)\cong {\mathbb Z}/p\{1,\alpha_{ij},\alpha\}$
. Of course
$H^*(BG)/(p,y_1,y_2,y_3)\cong {\mathbb Z}/p\{1,\alpha_{ij},\alpha\}$
. Of course
![]() $1\not \in N^1H^*(X)$
, we have the theorem from Lemma 4·1.
$1\not \in N^1H^*(X)$
, we have the theorem from Lemma 4·1.
Theorem 5·2.
Let
![]() $X=X(N)_n$
be an approximation for
$X=X(N)_n$
be an approximation for
![]() $(B{\mathbb Z}/p)^n$
with
$(B{\mathbb Z}/p)^n$
with
![]() $N>|Q_0Q_1...Q_{n-1}(x_1...x_n)|$
. Then we have for
$N>|Q_0Q_1...Q_{n-1}(x_1...x_n)|$
. Then we have for
![]() $\alpha_{i_1,...,i_s}=Q_0(x_{i_1}...x_{i_s})$
,
$\alpha_{i_1,...,i_s}=Q_0(x_{i_1}...x_{i_s})$
,
Here the notation
![]() $DH^*(X)\supset B^*$
means
$DH^*(X)\supset B^*$
means
![]() $DH^t(X)\supset B^t$
for the degree t-homogeneous parts of B for all
$DH^t(X)\supset B^t$
for the degree t-homogeneous parts of B for all
![]() $t<N$
strictly speaking.
$t<N$
strictly speaking.
Proof. We have the theorem from Lemma 4·3 and
![]() $ Q_{i_1}...Q_{i_{s-2}}(\alpha_{i_1,...,i_s})$
is
$ Q_{i_1}...Q_{i_{s-2}}(\alpha_{i_1,...,i_s})$
is
(Note the
![]() $n=|\alpha^{\prime}|$
in Lemma 4·3 is written by
$n=|\alpha^{\prime}|$
in Lemma 4·3 is written by
![]() $s-1$
here.)
$s-1$
here.)
Corollary 5·3.
If
![]() $n\not =m\ge 3$
, then
$n\not =m\ge 3$
, then
![]() $X(N)_n$
and
$X(N)_n$
and
![]() $X(N)_m$
are not stable birational equivalent.
$X(N)_m$
are not stable birational equivalent.
Next we study small non-abelian p-groups. Let G be a non-abelian group of order
![]() $p^3$
(see Section 8, for details). Then
$p^3$
(see Section 8, for details). Then
![]() $H^{even}(BG)$
is generated by Chern classes, and
$H^{even}(BG)$
is generated by Chern classes, and
![]() $H^{odd}(BG)$
is a (just) p-torsion. We can identify
$H^{odd}(BG)$
is a (just) p-torsion. We can identify
![]() $H^{odd}(BG)\subset H^{odd}(BG;\,{\mathbb Z}/p)$
.The operation
$H^{odd}(BG)\subset H^{odd}(BG;\,{\mathbb Z}/p)$
.The operation
![]() $Q_1$
acts on
$Q_1$
acts on
![]() $H^{odd}(X)$
, and induces the injection
$H^{odd}(X)$
, and induces the injection
Such groups are four types (see Section 8 below), and they are called extraspecial p-groups
![]() $G=p_{\pm}^{1+2}$
of order
$G=p_{\pm}^{1+2}$
of order
![]() $p^3$
. When
$p^3$
. When
![]() $G=Q_8=2_-^{1+2}$
the quaternion group of order 8, we know
$G=Q_8=2_-^{1+2}$
the quaternion group of order 8, we know
![]() $H^{odd}(X)=0$
. However when
$H^{odd}(X)=0$
. However when
![]() $G=D_8=2_+^{1+2}$
the dihedral group of order 8, the cohomology
$G=D_8=2_+^{1+2}$
the dihedral group of order 8, the cohomology
![]() $H^{odd}(BG)$
is generated as an
$H^{odd}(BG)$
is generated as an
![]() $H^{even}(BG)$
module by an element e of
$H^{even}(BG)$
module by an element e of
![]() $deg(e)=3$
. When
$deg(e)=3$
. When
![]() $G=E=p_+^{1+2}$
for
$G=E=p_+^{1+2}$
for
![]() $p\ge 3$
,
$p\ge 3$
,
![]() $H^{odd}(BG)$
is generated by
$H^{odd}(BG)$
is generated by
![]() $e_1,e_2$
with
$e_1,e_2$
with
![]() $deg(e_i)=3$
. When
$deg(e_i)=3$
. When
![]() $G=M=p_-^{1+2}$
for
$G=M=p_-^{1+2}$
for
![]() $p\ge 3$
,
$p\ge 3$
,
![]() $H^{odd}(BG)$
is generated by e
′ but
$H^{odd}(BG)$
is generated by e
′ but
![]() $deg(e^{\prime})=2p+1$
.
$deg(e^{\prime})=2p+1$
.
From Lemma 3·5 (Frobenius reciprocity) and the main lemma (Lemma 4·1), we have the following theorem.
Theorem 5·4.
Let
![]() $X=X(N)$
with
$X=X(N)$
with
![]() $N>2p+3$
be an approximation for an extraspecial p-group G of order
$N>2p+3$
be an approximation for an extraspecial p-group G of order
![]() $p^3$
. Then we have for all
$p^3$
. Then we have for all
![]() $*<N$
:
$*<N$
:
 \begin{equation*} DH^*(X)\cong\begin{cases} 0\quad for \ G=Q_8\\[3pt] {\mathbb Z}/2\{e\}\quad for \ G=D_8\\[3pt] 0\ or \ {\mathbb Z}/p\{e^{\prime}\} \quad for\ G=M \\[3pt] {\mathbb Z}/p\{e_1,e_2\} \quad for \ G=E.\end{cases} \end{equation*}
\begin{equation*} DH^*(X)\cong\begin{cases} 0\quad for \ G=Q_8\\[3pt] {\mathbb Z}/2\{e\}\quad for \ G=D_8\\[3pt] 0\ or \ {\mathbb Z}/p\{e^{\prime}\} \quad for\ G=M \\[3pt] {\mathbb Z}/p\{e_1,e_2\} \quad for \ G=E.\end{cases} \end{equation*}
In particular, the above theorem implies that when
![]() $G=p_+^{1+2}$
, all
$G=p_+^{1+2}$
, all
![]() $X=X(N)$
satisfy
$X=X(N)$
satisfy
![]() $DH^3(X)\not =0$
but
$DH^3(X)\not =0$
but
![]() $ DH^*(X)=0$
for all
$ DH^*(X)=0$
for all
![]() $4\le *<N.$
$4\le *<N.$
In this paper, we can not decide
![]() $DH^*(X)$
when
$DH^*(X)$
when
![]() $G=M$
.
$G=M$
.
6. Connected groups
At first, we consider when
![]() $G=U_n$
,
$G=U_n$
,
![]() $SU_n$
or
$SU_n$
or
![]() $Sp_{2n}$
for all p, where the cohomology
$Sp_{2n}$
for all p, where the cohomology
![]() $H^*(BG)$
has no torsion. Then
$H^*(BG)$
has no torsion. Then
![]() $H^*(BG)$
is generated by Chern classes, e.g.,
$H^*(BG)$
is generated by Chern classes, e.g.,
Hence
![]() $DH^*(X)=0$
for the approximations X for these groups.
$DH^*(X)=0$
for the approximations X for these groups.
Next we consider the case
![]() $G=SO_3$
and
$G=SO_3$
and
![]() $p=2$
. Then
$p=2$
. Then
where
![]() $w_i$
is the ith Stiefel–Whitney class for
$w_i$
is the ith Stiefel–Whitney class for
![]() $SO_3\subset O_3$
and
$SO_3\subset O_3$
and
![]() $w_i^2=c_i$
is the ith Chern class for
$w_i^2=c_i$
is the ith Chern class for
![]() $SO_3\subset U_3$
. (Also it is the elementary symmetric polynomial in
$SO_3\subset U_3$
. (Also it is the elementary symmetric polynomial in
![]() ${\mathbb Z}/2[y_1,...,y_i]$
.)
${\mathbb Z}/2[y_1,...,y_i]$
.)
Here we know
![]() $Q_0(w_2)=w_3,$
and
$Q_0(w_2)=w_3,$
and
![]() $Q_1(w_3)=w_3^2=c_3$
. Therefore we have [
Reference Yagita22
]
$Q_1(w_3)=w_3^2=c_3$
. Therefore we have [
Reference Yagita22
]
In particular
![]() $H^*(BG)/2\cong Ker(Q_0)\cong {\mathbb Z}/2[c_2,c_3]\{1,w_3\}. $
Then from Lemma 4·1, we have
$H^*(BG)/2\cong Ker(Q_0)\cong {\mathbb Z}/2[c_2,c_3]\{1,w_3\}. $
Then from Lemma 4·1, we have
Theorem 6·1.
Let
![]() $G=SO_3$
and X be an approximation of BG for
$G=SO_3$
and X be an approximation of BG for
![]() $6<N$
. Then
$6<N$
. Then
![]() $DH^*(X)\cong{\mathbb Z}/2\{w_3\}$
for
$DH^*(X)\cong{\mathbb Z}/2\{w_3\}$
for
![]() $*<N.$
$*<N.$
Using Lemma 4·3, we have
Theorem 6·2.
Let
![]() $X_n=X_n(N)$
be approximations for
$X_n=X_n(N)$
be approximations for
![]() $BSO_n$
for
$BSO_n$
for
![]() $n\ge 3$
. Moreover, let
$n\ge 3$
. Moreover, let
![]() $|Q_1...Q_{2m-1}(w_{2m+1})|<N$
. Then we have
$|Q_1...Q_{2m-1}(w_{2m+1})|<N$
. Then we have
Proof. Since
![]() $Q_0w_{2i}=w_{2i+1}$
, we see
$Q_0w_{2i}=w_{2i+1}$
, we see
![]() $w_{2i+1}\in N^1H^{2i+1}(X)$
from Lemma 3·7. We have the theorem, from Lemma 4·3 and the restriction to
$w_{2i+1}\in N^1H^{2i+1}(X)$
from Lemma 3·7. We have the theorem, from Lemma 4·3 and the restriction to
![]() $H^*(B({\mathbb Z}/2)^{2i};\,{\mathbb Z}/2),$
$H^*(B({\mathbb Z}/2)^{2i};\,{\mathbb Z}/2),$
Remark. The same inclusion
holds for
![]() $G=SO_{2m+2}$
. Since
$G=SO_{2m+2}$
. Since
![]() $O_{2m+1}\cong SO_{2m+1}\times {\mathbb Z}/2$
, the orthogonal group
$O_{2m+1}\cong SO_{2m+1}\times {\mathbb Z}/2$
, the orthogonal group
![]() $O_{2m+1}$
(hence
$O_{2m+1}$
(hence
![]() $O_{2m+2}$
) also has the same property.
$O_{2m+2}$
) also has the same property.
We next consider simply connected groups. Let us write by X an approximation for
![]() $BG_2$
for the exceptional simple group
$BG_2$
for the exceptional simple group
![]() $G_2$
of
$G_2$
of
![]() $rank=2$
. The mod (2) cohomology is generated by the Stiefel–Whitney classes
$rank=2$
. The mod (2) cohomology is generated by the Stiefel–Whitney classes
![]() $w_i$
of the real representation
$w_i$
of the real representation
![]() $G_2\to SO_7$
$G_2\to SO_7$
Then we have
![]() $Q_1w_4=w_7, Q_2(w_7)=w_7^2=c_7$
(the Chern class).
$Q_1w_4=w_7, Q_2(w_7)=w_7^2=c_7$
(the Chern class).
The Chow ring of
![]() $BG_2$
is also known
$BG_2$
is also known
In particular the cycle map
![]() $cl\,:\, CH^*(BG)\to H^*(BG)$
is injective.
$cl\,:\, CH^*(BG)\to H^*(BG)$
is injective.
It is known
![]() $w_4\in N^1H^*(X;\,{\mathbb Z}/2)$
([
Reference Yagita22
]) and from Lemma 3·2, we see
$w_4\in N^1H^*(X;\,{\mathbb Z}/2)$
([
Reference Yagita22
]) and from Lemma 3·2, we see
![]() $w_4\in N^1H^*(X)$
. Since
$w_4\in N^1H^*(X)$
. Since
![]() $Q_1(w_4)=w_7\not =0$
, from Lemma 4·1, we have
$Q_1(w_4)=w_7\not =0$
, from Lemma 4·1, we have
![]() $DH^4(X)\not =0$
. This fact is known in [
Reference Benoist and Ottem1
]. Moreover
$DH^4(X)\not =0$
. This fact is known in [
Reference Benoist and Ottem1
]. Moreover
![]() $H^*(BG)/(c_4,c_6,c_7)\cong\Lambda(w_4,w_7)$
implies:
$H^*(BG)/(c_4,c_6,c_7)\cong\Lambda(w_4,w_7)$
implies:
Proposition 6·3.
For X an approximation for
![]() $BG_2$
, we have the surjection
$BG_2$
, we have the surjection
By Voevodsky [
Reference Voevodsky18
,
Reference Voevodsky19
], we have the
![]() $Q_i$
operation also in the motivic cohomology
$Q_i$
operation also in the motivic cohomology
![]() $H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$
with
$H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$
with
![]() $deg(Q_i)=(2p^i-1,p-1)$
. Then we can take
$deg(Q_i)=(2p^i-1,p-1)$
. Then we can take
By Theorem 3·1, the above means
We cannot see here that
![]() $0\not =w_7\in DH^*(X)$
, but see the following proposition.
$0\not =w_7\in DH^*(X)$
, but see the following proposition.
Proposition 6·4.
Let
![]() $N>|Q_2w_7|=14$
. For an approximation
$N>|Q_2w_7|=14$
. For an approximation
![]() $X=X(N)$
for
$X=X(N)$
for
![]() $BG_2$
, we have
$BG_2$
, we have
Proof. Suppose
![]() $w_7\in \tilde N^3H^*(X)$
. That is, there is
$w_7\in \tilde N^3H^*(X)$
. That is, there is
![]() $x\in H^1(Y)$
with
$x\in H^1(Y)$
with
![]() $f_*(x)=w_7$
for
$f_*(x)=w_7$
for
![]() $f\,:\,Y\to X$
. Act
$f\,:\,Y\to X$
. Act
![]() $Q_2$
on
$Q_2$
on
![]() $H^*(Y;\,{\mathbb Z}/2)$
, and
$H^*(Y;\,{\mathbb Z}/2)$
, and
since
![]() $\beta(x)=0$
and
$\beta(x)=0$
and
![]() $P^{i}(x)=Sq^{2i}(x)=0$
for
$P^{i}(x)=Sq^{2i}(x)=0$
for
![]() $i>0$
. But
$i>0$
. But
![]() $Q_2w_7=c_7\not =0$
. This contradicts to the commutativity of
$Q_2w_7=c_7\not =0$
. This contradicts to the commutativity of
![]() $f_*$
and
$f_*$
and
![]() $Q_2$
.
$Q_2$
.
Theorem 6·5.
Let G be a simply connected group such that
![]() $H^*(BG)$
has p-torsion. Let
$H^*(BG)$
has p-torsion. Let
![]() $X=X(N)$
be an approximation for BG for
$X=X(N)$
be an approximation for BG for
![]() $N\ge 2p+3$
. Then
$N\ge 2p+3$
. Then
![]() $ DH^4(X)\not =0$
.
$ DH^4(X)\not =0$
.
Proof. We only need to prove the theorem when G is a simple group having p torsion in
![]() $H^*(BG)$
. Let
$H^*(BG)$
. Let
![]() $p=2$
. It is well known that there is an embedding
$p=2$
. It is well known that there is an embedding
![]() $j\,:\,G_2\subset G$
such that (see [
Reference Pirutka and Yagita10
,
Reference Yagita25
] for details)
$j\,:\,G_2\subset G$
such that (see [
Reference Pirutka and Yagita10
,
Reference Yagita25
] for details)
Let
![]() $x=(j^{*})^{-1}w_4\in H^4(BG)$
. From [
Reference Yagita25
, lemma 3·1], we see that 2x is represented by Chern classes. Hence 2x is the image from
$x=(j^{*})^{-1}w_4\in H^4(BG)$
. From [
Reference Yagita25
, lemma 3·1], we see that 2x is represented by Chern classes. Hence 2x is the image from
![]() $CH^*(X)$
, and so
$CH^*(X)$
, and so
![]() $2x\in N^1H^4(X)$
. This means there is an open set
$2x\in N^1H^4(X)$
. This means there is an open set
![]() $U\subset X$
such that
$U\subset X$
such that
![]() $ 2x=0\in H^*(U)$
that is. x is 2-torsion in
$ 2x=0\in H^*(U)$
that is. x is 2-torsion in
![]() $H^*(U)$
. Hence from Lemma 3·5, we have
$H^*(U)$
. Hence from Lemma 3·5, we have
![]() $x\in N^1H^4(U)$
, and so there is
$x\in N^1H^4(U)$
, and so there is
![]() $U^{\prime}\subset U$
such that
$U^{\prime}\subset U$
such that
![]() $x=0\in H^4(U^{\prime})$
. This implies
$x=0\in H^4(U^{\prime})$
. This implies
![]() $x\in N^1H^4(X)$
.
$x\in N^1H^4(X)$
.
Since
![]() $j^*(Q_1x)=Q_1w_4=w_7$
, we see
$j^*(Q_1x)=Q_1w_4=w_7$
, we see
![]() $Q_1x\not =0$
. From the main lemma (Lemma 4·1), we see
$Q_1x\not =0$
. From the main lemma (Lemma 4·1), we see
![]() $DH^4(X)\not =0$
for G.
$DH^4(X)\not =0$
for G.
For the cases
![]() $p=3,5$
, we consider the exceptional groups
$p=3,5$
, we consider the exceptional groups
![]() $F_4,E_8$
respectively. Each simply connected simple group G contains
$F_4,E_8$
respectively. Each simply connected simple group G contains
![]() $F_4$
for
$F_4$
for
![]() $p=3$
,
$p=3$
,
![]() $E_8$
for
$E_8$
for
![]() $p=5$
. There is
$p=5$
. There is
![]() $x\in H^4(BG)$
such that px is a Chern class [
Reference Yagita25
], and
$x\in H^4(BG)$
such that px is a Chern class [
Reference Yagita25
], and
![]() $Q_1(x)\not =0\in H^*(BG;\,{\mathbb Z}/p).$
In fact, there is embedding
$Q_1(x)\not =0\in H^*(BG;\,{\mathbb Z}/p).$
In fact, there is embedding
![]() $j\,:\,({\mathbb Z}/p)^3\subset G$
with
$j\,:\,({\mathbb Z}/p)^3\subset G$
with
![]() $j^*(x)=Q_0(x_1x_2x_3)$
. Hence we have the theorem.
$j^*(x)=Q_0(x_1x_2x_3)$
. Hence we have the theorem.
Corollary 6·6.
Let X be an approximation for
![]() $BSpin_n$
with
$BSpin_n$
with
![]() $n\ge 7$
or BG for an exceptional group G. Then X is not stable rational.
$n\ge 7$
or BG for an exceptional group G. Then X is not stable rational.
Remark. Kordonskii [
Reference Kordonskii6
], Merkurjev ([
Reference Merkurjev7
, corollary 5·8]), and Reichstein–Scavia show [
Reference Reichstein and Scavia14
] that the classifying space
![]() $BSpin_n$
itself is stably rational when
$BSpin_n$
itself is stably rational when
![]() $n\le 14$
. Hence the (Ekedahl) approximation X is not stable rationally equivalent to BG. In fact, these X is constructed from a quasi projective variety BG as taking intersections of subspaces of
$n\le 14$
. Hence the (Ekedahl) approximation X is not stable rationally equivalent to BG. In fact, these X is constructed from a quasi projective variety BG as taking intersections of subspaces of
![]() ${\mathbb P}^{M}$
for a large M. (The author thanks Federico Scavia who pointed out this remark.)
${\mathbb P}^{M}$
for a large M. (The author thanks Federico Scavia who pointed out this remark.)
At last of this section, we consider the case
![]() $G=PGL_p$
. We have (for example [
Reference Kameko and Yagita5
, theorems 1·5, 1·7]) additively
$G=PGL_p$
. We have (for example [
Reference Kameko and Yagita5
, theorems 1·5, 1·7]) additively
where
![]() $x_{2p+2}=Q_1Q_0u_2$
and suffix means its degree. The Chow ring is given as
$x_{2p+2}=Q_1Q_0u_2$
and suffix means its degree. The Chow ring is given as
From Lemma 4·1, we have:
Theorem 6·7.
Let p be odd. For an approximation X for
![]() $BPGL_p$
, we see
$BPGL_p$
, we see
![]() $ {\mathbb Z}/p\{Q_0u_2\}\subset DH^*(X)$
, and moreover there is a surjection
$ {\mathbb Z}/p\{Q_0u_2\}\subset DH^*(X)$
, and moreover there is a surjection
for the cycle map
![]() $cl\,:\,CH^*(X)\to H^{2*}(X)$
.
$cl\,:\,CH^*(X)\to H^{2*}(X)$
.
In the above case, we do not see here that
![]() $DH^*(X)$
for
$DH^*(X)$
for
![]() $*<N$
is invariant of BG. (See the remark in the introduction.)
$*<N$
is invariant of BG. (See the remark in the introduction.)
7.
 ${\mathbb Z}/p$
-coefficient cohomology for abelian groups
${\mathbb Z}/p$
-coefficient cohomology for abelian groups
In the preceding sections, we have seen that cases
![]() $DH^*(X;\,A)\not =0$
are not so rare for
$DH^*(X;\,A)\not =0$
are not so rare for
![]() $A={\mathbb Z}_{(p)}$
,
$A={\mathbb Z}_{(p)}$
,
![]() ${\mathbb Z}/p^i$
,
${\mathbb Z}/p^i$
,
![]() $i\ge 2$
. However currently it seems difficult to make such example for
$i\ge 2$
. However currently it seems difficult to make such example for
![]() $A={\mathbb Z}/p$
. (Recall the final remark in Section 4.)
$A={\mathbb Z}/p$
. (Recall the final remark in Section 4.)
Question 7·1. Is
![]() $DH^*(X;\,{\mathbb Z}/p)=0$
for each smooth projective variety X?
$DH^*(X;\,{\mathbb Z}/p)=0$
for each smooth projective variety X?
At first, we consider the case
![]() $G=({\mathbb Z}/p)^3$
.
$G=({\mathbb Z}/p)^3$
.
Lemma 7·2.
Let
![]() $X=X(N), N>3$
be an approximation for
$X=X(N), N>3$
be an approximation for
![]() $(B{\mathbb Z}/p)^3$
. Then we have
$(B{\mathbb Z}/p)^3$
. Then we have
![]() $DH^*(X;\,{\mathbb Z}/p)=0$
for all
$DH^*(X;\,{\mathbb Z}/p)=0$
for all
![]() $*<N.$
$*<N.$
Proof. Recall the mod p cohomology
Here
![]() $y_i$
is a Chern class. Hence
$y_i$
is a Chern class. Hence
![]() $x_jy_i=0 \in DH^*(X;\,{\mathbb Z}/p)$
by reciprocity law. Hence we only need to check it for
$x_jy_i=0 \in DH^*(X;\,{\mathbb Z}/p)$
by reciprocity law. Hence we only need to check it for
![]() $z\in \Lambda(x_1,x_2,x_3)$
. But these
$z\in \Lambda(x_1,x_2,x_3)$
. But these
![]() $z\not \in N^1H^*(X;\,{\mathbb Z}/p)$
(see Lemma 7·4 below). Hence
$z\not \in N^1H^*(X;\,{\mathbb Z}/p)$
(see Lemma 7·4 below). Hence
![]() $DH^*(X;\,{\mathbb Z}/p)=0$
.
$DH^*(X;\,{\mathbb Z}/p)=0$
.
Example of Gysin maps. We can take a quasi projective approximation
![]() $\bar X(N)$
of
$\bar X(N)$
of
![]() $B{\mathbb Z}/p$
explicitly by the quotient (the N-dimensional lens space)
$B{\mathbb Z}/p$
explicitly by the quotient (the N-dimensional lens space)
Next we consider the projective approximation
Let us write
![]() $X_i$
(resp.
$X_i$
(resp.
![]() $X^{\prime}_i$
) for
$X^{\prime}_i$
) for
![]() $i=1,2,3$
the above
$i=1,2,3$
the above
![]() $\bar X(N)$
(resp.
$\bar X(N)$
(resp.
![]() $\bar X(N-1))$
for a sufficient large number N. Let
$\bar X(N-1))$
for a sufficient large number N. Let
Similarly we define
![]() $Y_2,Y_3$
, and the disjoin union
$Y_2,Y_3$
, and the disjoin union
![]() $Y=Y_1\sqcup Y_2\sqcup Y_3$
.
$Y=Y_1\sqcup Y_2\sqcup Y_3$
.
Recall that for
![]() $p\,:\,odd$
$p\,:\,odd$
and
![]() $H^*(Y_i;\,{\mathbb Z}/p)\cong H^*(X;\,{\mathbb Z}/p)/\left(y_i^N\right)$
for
$H^*(Y_i;\,{\mathbb Z}/p)\cong H^*(X;\,{\mathbb Z}/p)/\left(y_i^N\right)$
for
![]() $i=1,2,3$
. For
$i=1,2,3$
. For
![]() $p=2$
, some graded ring
$p=2$
, some graded ring
![]() $grH^*(X;\,{\mathbb Z}/2)$
is isomorphic to the above ring (in fact
$grH^*(X;\,{\mathbb Z}/2)$
is isomorphic to the above ring (in fact
![]() $x^2_i=y_i$
).
$x^2_i=y_i$
).
For the embedding
![]() $f_i\,:\,X^{\prime}_i\to X_i$
, it is known
$f_i\,:\,X^{\prime}_i\to X_i$
, it is known
![]() $f_{i*}(1)=c_1(N_i)$
where
$f_{i*}(1)=c_1(N_i)$
where
![]() $N_i$
is the normal bundle for
$N_i$
is the normal bundle for
![]() $X^{\prime}_i\subset X_i$
. Hence the Gysin map is given by
$X^{\prime}_i\subset X_i$
. Hence the Gysin map is given by
Therefore we have for
![]() $x=(x_2x_3+ x_3x_1+x_1x_2)\in H^*(Y_1\sqcup Y_2\sqcup Y_3;\,{\mathbb Z}/p)$
,
$x=(x_2x_3+ x_3x_1+x_1x_2)\in H^*(Y_1\sqcup Y_2\sqcup Y_3;\,{\mathbb Z}/p)$
,
(Note that the element
![]() $x=(x_1x_2+x_2x_3+x_3x_1)$
is not in the integral cohomology
$x=(x_1x_2+x_2x_3+x_3x_1)$
is not in the integral cohomology
![]() $H^*(Y)$
.) Thus we see
$H^*(Y)$
.) Thus we see
![]() $\alpha\in \tilde N^cH^*(X;\,{\mathbb Z}/p).$
More generally, we see
$\alpha\in \tilde N^cH^*(X;\,{\mathbb Z}/p).$
More generally, we see
Theorem 7·3.
Let
![]() $X=X(N)$
be an approximation for
$X=X(N)$
be an approximation for
![]() $(B{\mathbb Z}/p)^n$
with
$(B{\mathbb Z}/p)^n$
with
![]() ${\mathbb Z}/p$
-coefficients. Then we have
${\mathbb Z}/p$
-coefficients. Then we have
We recall here the motivic cohomology. By Voevodsky [
Reference Voevodsky18
],
![]() $H^{*,*^{\prime}}(B{\mathbb Z}/p;\,{\mathbb Z}/p)$
satisfies the K
$H^{*,*^{\prime}}(B{\mathbb Z}/p;\,{\mathbb Z}/p)$
satisfies the K
![]() $\ddot{{u}}$
nneth formula so that (for p odd)
$\ddot{{u}}$
nneth formula so that (for p odd)
Here
![]() $0\not =\tau\in H^{0,1}(Spec({\mathbb C});\,{\mathbb Z}/p)$
, and
$0\not =\tau\in H^{0,1}(Spec({\mathbb C});\,{\mathbb Z}/p)$
, and
![]() $deg(y_i)=(2,1)$
,
$deg(y_i)=(2,1)$
,
![]() $deg(x_i)=(1,1)$
.
$deg(x_i)=(1,1)$
.
From Lemma 3·1, we can identify
![]() $N^cH_{et}^*(X;\,{\mathbb Z}/p)= F_{\tau}^{*,*-c}$
where
$N^cH_{et}^*(X;\,{\mathbb Z}/p)= F_{\tau}^{*,*-c}$
where
![]() $F_{\tau}^{*,*-c}=Im(\times \tau^c\,:\,H^{*,*-c}(X;\,{\mathbb Z}/p)\to H^{*,*}(X;\,{\mathbb Z}/p)).$
$F_{\tau}^{*,*-c}=Im(\times \tau^c\,:\,H^{*,*-c}(X;\,{\mathbb Z}/p)\to H^{*,*}(X;\,{\mathbb Z}/p)).$
Lemma 7·4. ([
Reference Tezuka and Yagita16
, theorem 5·1]) Let
![]() $X=X(N)$
be an approximation for
$X=X(N)$
be an approximation for
![]() $(B{\mathbb Z}/p)^n$
for a sufficient large N. Then we have
$(B{\mathbb Z}/p)^n$
for a sufficient large N. Then we have
Proof. Let
![]() $x\in Ideal(y_1,...,y_n)\subset H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$
. Then
$x\in Ideal(y_1,...,y_n)\subset H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$
. Then
![]() $deg(x)=(*,*^{\prime})$
with
$deg(x)=(*,*^{\prime})$
with
![]() $*>*^{\prime}$
, and x is a multiplying of
$*>*^{\prime}$
, and x is a multiplying of
![]() $\tau$
. Hence
$\tau$
. Hence
![]() $x\in N^1H^*(X;\,{\mathbb Z}/p)$
.
$x\in N^1H^*(X;\,{\mathbb Z}/p)$
.
Proof of Theorem 7·3. Let
![]() $x\in N^1H^*(X;\,{\mathbb Z}/p)$
. From the above lemma,
$x\in N^1H^*(X;\,{\mathbb Z}/p)$
. From the above lemma,
![]() $x\in Ideal(y_1,...,y_n)$
which is in the image of the Gysin map. That is
$x\in Ideal(y_1,...,y_n)$
which is in the image of the Gysin map. That is
![]() $x\in \tilde N^1H^*(X;\,{\mathbb Z}/p)$
.
$x\in \tilde N^1H^*(X;\,{\mathbb Z}/p)$
.
We can extend Theorem 7·3, by using the following lemma. Let us write by XG an approximation for BG. Let
![]() $j\,:\, BS\to BG$
and
$j\,:\, BS\to BG$
and
![]() $i;\, Y\to XS$
. We consider maps:
$i;\, Y\to XS$
. We consider maps:
Lemma 7·5.
Let G have a Sylow p-subgroup S. If
![]() $ DH^*(XS;\,{\mathbb Z}/p)=0$
, then
$ DH^*(XS;\,{\mathbb Z}/p)=0$
, then
![]() $DH^*(XG\,:\,{\mathbb Z}/p)=0$
also for BG.
$DH^*(XG\,:\,{\mathbb Z}/p)=0$
also for BG.
Proof. Let
![]() $j\,:\, BS\to BG$
so that
$j\,:\, BS\to BG$
so that
![]() $j_*=cor_S^G$
is the transfer (with the codimension
$j_*=cor_S^G$
is the transfer (with the codimension
![]() $c=0$
) for finite groups. Note that
$c=0$
) for finite groups. Note that
![]() $j^*N^1H^*(XG;\,{\mathbb Z}/p)\subset N^1H^*(XS;\,{\mathbb Z}/p)$
by the naturality of
$j^*N^1H^*(XG;\,{\mathbb Z}/p)\subset N^1H^*(XS;\,{\mathbb Z}/p)$
by the naturality of
![]() $j^*$
. Hence given
$j^*$
. Hence given
![]() $x\in N^1H^*(XG;\,{\mathbb Z}/p)$
, the element
$x\in N^1H^*(XG;\,{\mathbb Z}/p)$
, the element
![]() $y=j^*(x)$
is in
$y=j^*(x)$
is in
![]() $N^1H^*(XS;\,{\mathbb Z}/p)$
.
$N^1H^*(XS;\,{\mathbb Z}/p)$
.
By the assumption in this lemma, there are
![]() $i\,:\,Y\to XS$
and y
′ such that
$i\,:\,Y\to XS$
and y
′ such that
![]() $y^{\prime}\in H^*(Y;\,{\mathbb Z}/p)$
with
$y^{\prime}\in H^*(Y;\,{\mathbb Z}/p)$
with
![]() $i_*(y^{\prime})=y$
. We consider maps:
$i_*(y^{\prime})=y$
. We consider maps:
Then we have
![]() $\ j_*i_*(y^{\prime})=j_*y=j_*j^*(x)=[G;\,S]x.$
$\ j_*i_*(y^{\prime})=j_*y=j_*j^*(x)=[G;\,S]x.$
Similarly, we can prove:
Corollary 7·6.
Let G have an abelian Sylow p-subgroup. Let
![]() $X=X(N)$
be an approximation for BG. Then we have
$X=X(N)$
be an approximation for BG. Then we have
![]() $ DH^*(X;\,{\mathbb Z}/p)=0$
for all
$ DH^*(X;\,{\mathbb Z}/p)=0$
for all
![]() $ *<N$
.
$ *<N$
.
8. The groups
 $Q_8$
and
$Q_8$
and
 $D_8$
$D_8$
When
![]() $|G|=p^3$
, we have the short exact sequence
$|G|=p^3$
, we have the short exact sequence
where
![]() $C\cong {\mathbb Z}/p$
is in the center and
$C\cong {\mathbb Z}/p$
is in the center and
![]() $ V\cong {\mathbb Z}/p\times {\mathbb Z}/p$
. Let us take generators such that
$ V\cong {\mathbb Z}/p\times {\mathbb Z}/p$
. Let us take generators such that
![]() $C={\langle} c{\rangle}, V={\langle} a,b {\rangle}.$
Moreover we can take
$C={\langle} c{\rangle}, V={\langle} a,b {\rangle}.$
Moreover we can take
![]() $[a,b]=c$
when G is non-abelian.
$[a,b]=c$
when G is non-abelian.
There are two cases, when
![]() $p=2$
, the quaternion group
$p=2$
, the quaternion group
![]() $Q_8$
and the dihedral group
$Q_8$
and the dihedral group
![]() $D_8$
. We will show here
$D_8$
. We will show here
Theorem 8·1.
Let
![]() $X=X(N)$
be an approximation for
$X=X(N)$
be an approximation for
![]() $Q_8$
or
$Q_8$
or
![]() $D_8$
. Then
$D_8$
. Then
![]() $DH^*(X;\,{\mathbb Z}/2)=0$
for all
$DH^*(X;\,{\mathbb Z}/2)=0$
for all
![]() $*<N$
.
$*<N$
.
8·1. The case
![]() $G=Q_8$
. Then
$G=Q_8$
. Then
![]() $a^2=b^2=c$
. Its cohomologies are well known (see [
Reference Quillen12
]):
$a^2=b^2=c$
. Its cohomologies are well known (see [
Reference Quillen12
]):
where
![]() $ x_i^2=y_i$
$ x_i^2=y_i$
![]() $|x_i|=1$
, and
$|x_i|=1$
, and
![]() $w=y_1x_2=y_2x_1$
,
$w=y_1x_2=y_2x_1$
,
![]() $|w|=3$
.
$|w|=3$
.
Therefore, we see
Of course
![]() $deg(x_i)=(1,1)$
in
$deg(x_i)=(1,1)$
in
![]() $H^{*,*^{\prime}}(BG;\,{\mathbb Z}/2)$
and they are not in
$H^{*,*^{\prime}}(BG;\,{\mathbb Z}/2)$
and they are not in
![]() $N^1H^*(BG;\,{\mathbb Z}/2)$
. Thus we have Theorem 8·1 for
$N^1H^*(BG;\,{\mathbb Z}/2)$
. Thus we have Theorem 8·1 for
![]() $G=Q_8$
.
$G=Q_8$
.
8·2. The case
![]() $G=D_8$
. Then
$G=D_8$
. Then
![]() $a^2=c, b^2=1$
. It is well known
$a^2=c, b^2=1$
. It is well known
The mod 2 cohomlogy is written [ Reference Quillen12 ]
Here
![]() $y_j=x_j^2, u^2=c_2$
and
$y_j=x_j^2, u^2=c_2$
and
![]() $Q_0(u)=(x_1+x_2)u=e,Q_1Q_0(u)=(y_1+y_2)c_2$
.
$Q_0(u)=(x_1+x_2)u=e,Q_1Q_0(u)=(y_1+y_2)c_2$
.
We note
![]() $y_1,y_2,c_2\in CH^*(BG)/2$
and
$y_1,y_2,c_2\in CH^*(BG)/2$
and
Moreover,
![]() $deg(x_j)=(1,1)$
,
$deg(x_j)=(1,1)$
,
![]() $deg(u)=(2,2)$
in the motivic cohomology
$deg(u)=(2,2)$
in the motivic cohomology
![]() $H^{*,*^{\prime}}(BG;\,{\mathbb Z}/2)$
and they are not in
$H^{*,*^{\prime}}(BG;\,{\mathbb Z}/2)$
and they are not in
![]() $N^1H^*(BG;\,{\mathbb Z}/2)$
. Here we note
$N^1H^*(BG;\,{\mathbb Z}/2)$
. Here we note
![]() $deg(x_ju)=(3,3)$
, but there is
$deg(x_ju)=(3,3)$
, but there is
![]() $u^{\prime}_j\in H^{3,2}(BG;\,{\mathbb Z}/2)$
with
$u^{\prime}_j\in H^{3,2}(BG;\,{\mathbb Z}/2)$
with
![]() $x_ju=\tau u^{\prime}_j$
from [
Reference Yagita24
, lemma 6·2] (i.e.,
$x_ju=\tau u^{\prime}_j$
from [
Reference Yagita24
, lemma 6·2] (i.e.,
![]() $x_ju\in N^1H^*(X;\,{\mathbb Z}/2)$
).
$x_ju\in N^1H^*(X;\,{\mathbb Z}/2)$
).
Hence for the proof of Lemma 8·1 (for
![]() $G=D_8$
), it is only needed to show
$G=D_8$
), it is only needed to show
Lemma 8·2.
Let
![]() $N>4$
and X be an approximation for BG. Then we have
$N>4$
and X be an approximation for BG. Then we have
![]() $x_iu\in \tilde N^1H^*(X;\,{\mathbb Z}/2)$
.
$x_iu\in \tilde N^1H^*(X;\,{\mathbb Z}/2)$
.
To prove the above lemma, for a G-variety H, we consider the equivariant cohomology (recall the arguments just before Lemma 3·6)
where E(N) is an (approximation of) contractible free G-variety. Let us write
For a closed embedding
![]() $i\,:\,H\subset K$
of G-varieties, we can define the Gysin map
$i\,:\,H\subset K$
of G-varieties, we can define the Gysin map
Hereafter in this section, let
![]() $G=D_8$
. We recall arguments in [
Reference Yagita24
]. We define the 2-dimensional representation
$G=D_8$
. We recall arguments in [
Reference Yagita24
]. We define the 2-dimensional representation
![]() $\tilde c\,:\, G\to U_2$
such that
$\tilde c\,:\, G\to U_2$
such that
![]() $\tilde c(a)=diag(i,-i)$
and
$\tilde c(a)=diag(i,-i)$
and
![]() $\bar c(b)$
is the permutation matrix (1,2). By this representation, we identify that
$\bar c(b)$
is the permutation matrix (1,2). By this representation, we identify that
![]() $W={\mathbb C}^{2*}={\mathbb C}^2-\{0\}$
is an G-variety. Note G acts freely on
$W={\mathbb C}^{2*}={\mathbb C}^2-\{0\}$
is an G-variety. Note G acts freely on
![]() $W\times {\mathbb C}^*$
but it does not act freely on
$W\times {\mathbb C}^*$
but it does not act freely on
![]() $W={\mathbb C}^{2*}.$
$W={\mathbb C}^{2*}.$
The fixed points set on W under b is
Similarly
![]() $W^{{\langle} bc{\rangle}}={\mathbb C}^*\{a^{-1}e^{\prime}\}.$
Take
$W^{{\langle} bc{\rangle}}={\mathbb C}^*\{a^{-1}e^{\prime}\}.$
Take
where
![]() $g\in GL_2({\mathbb C})$
with
$g\in GL_2({\mathbb C})$
with
![]() $g^{-1}bg=ab$
(note
$g^{-1}bg=ab$
(note
![]() $(ab)^2=1$
).
$(ab)^2=1$
).
Let us write
![]() $ H=H_0\sqcup H_1.$
Then G acts on
$ H=H_0\sqcup H_1.$
Then G acts on
![]() $H_i$
and acts freely on
$H_i$
and acts freely on
![]() ${\mathbb C}^{2*}-H$
. In fact it does not contain fixed points of non-trivial stabiliser groups. We consider the transfer for some G-variety H in
${\mathbb C}^{2*}-H$
. In fact it does not contain fixed points of non-trivial stabiliser groups. We consider the transfer for some G-variety H in
![]() ${\mathbb C}^{2*}$
, and induced equivariant cohomology
${\mathbb C}^{2*}$
, and induced equivariant cohomology
Lemma 8·3. We have
Proof. We consider the group extension
![]() $0\to {\langle} a{\rangle} \to G\to {\langle} b {\rangle} \to 0$
and the induced spectral sequence
$0\to {\langle} a{\rangle} \to G\to {\langle} b {\rangle} \to 0$
and the induced spectral sequence
Since
![]() ${\langle} a{\rangle}\cong {\mathbb Z}/4$
acts freely on
${\langle} a{\rangle}\cong {\mathbb Z}/4$
acts freely on
![]() $H_0$
, we see
$H_0$
, we see
![]() $H_0/{\langle} a{\rangle} \cong {\mathbb C}^{*}\{e^{\prime},ae^{\prime}\}/{\langle} a{\rangle}\cong {\mathbb C}^{*}.$
Therefore we have
$H_0/{\langle} a{\rangle} \cong {\mathbb C}^{*}\{e^{\prime},ae^{\prime}\}/{\langle} a{\rangle}\cong {\mathbb C}^{*}.$
Therefore we have
Since
![]() ${\langle} b{\rangle}$
acts trivially on
${\langle} b{\rangle}$
acts trivially on
![]() $\Lambda(z)$
we have this lemma
$\Lambda(z)$
we have this lemma
Note
![]() $H_G^*(H_0;\,{\mathbb Z}/2)\cong H_G^*(H_1;\,{\mathbb Z}/2)$
and hence we see
$H_G^*(H_0;\,{\mathbb Z}/2)\cong H_G^*(H_1;\,{\mathbb Z}/2)$
and hence we see
We consider the long exact sequence
and we have
![]() $H^*_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)\cong H^*(BG;\,{\mathbb Z}/2)/(c_2)$
. Hence, we get
$H^*_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)\cong H^*(BG;\,{\mathbb Z}/2)/(c_2)$
. Hence, we get
Now we consider the transfer
![]() $H^*_G(H;\,{\mathbb Z}/2) \stackrel{i_*}{\to} H^{*+2}_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)$
. We have explicitly ([
Reference Yagita24
, p. 527])
$H^*_G(H;\,{\mathbb Z}/2) \stackrel{i_*}{\to} H^{*+2}_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)$
. We have explicitly ([
Reference Yagita24
, p. 527])
Therefore we have Lemma 8·2 and hence Theorem 8·1 for
![]() $G=D_8$
.
$G=D_8$
.
To see the above
![]() $i_*$
, we recall the long exact sequence for
$i_*$
, we recall the long exact sequence for
![]() $i\,:\,H \subset {\mathbb C}^{2*}$
$i\,:\,H \subset {\mathbb C}^{2*}$
The transfer
![]() $i_*$
is determined by the following lemma.
$i_*$
is determined by the following lemma.
Lemma 8·4.
In the above
![]() $({**})$
, we see
$({**})$
, we see
![]() $\delta=0$
, and hence
$\delta=0$
, and hence
![]() $i_*$
is injective.
$i_*$
is injective.
Proof. Since G acts freely on
![]() ${\mathbb C}^{2*}-H$
, we have
${\mathbb C}^{2*}-H$
, we have
which is zero when
![]() $*>4=2dim(({\mathbb C}^{2*}-H)/G)$
. Hence
$*>4=2dim(({\mathbb C}^{2*}-H)/G)$
. Hence
![]() $\delta$
must be zero for
$\delta$
must be zero for
![]() $*>4$
, and
$*>4$
, and
![]() $i_*$
is injective for
$i_*$
is injective for
![]() $*>4$
. In particular,
$*>4$
. In particular,
![]() $i_*\left(y^2_jz_j\right)=y_j^2u^{\prime}_j$
. Since
$i_*\left(y^2_jz_j\right)=y_j^2u^{\prime}_j$
. Since
![]() $H^*_G(H;\,{\mathbb Z}/2)$
is
$H^*_G(H;\,{\mathbb Z}/2)$
is
![]() ${\mathbb Z}/2[y_1]$
-free (or
${\mathbb Z}/2[y_1]$
-free (or
![]() $Z/2[y_2]$
-free,) we see
$Z/2[y_2]$
-free,) we see
![]() $i_*(z_j)=u^{\prime}_j$
.
$i_*(z_j)=u^{\prime}_j$
.
Acknowledgement
The author thanks the referee very much for many comments and suggestions.