Article contents
Decoupling Decorations on Moduli Spaces of Manifolds
Published online by Cambridge University Press: 10 May 2022
Abstract
We study moduli spaces of d-dimensional manifolds with embedded particles and discs, which we refer to as decorations. These spaces admit a model in which points are unparametrised d-dimensional manifolds in 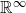 $\mathbb{R}^\infty$ with particles and discs constrained to it. We compare this to the space of d-dimensional manifolds in
$\mathbb{R}^\infty$ with particles and discs constrained to it. We compare this to the space of d-dimensional manifolds in 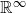 $\mathbb{R}^\infty$ with particles and discs that are no longer constrained, i.e. the decorations are decoupled. We show that under certain conditions these spaces cannot be distinguished by homology groups within a range. This generalises work by Bödigheimer–Tillmann for oriented surfaces to different tangential structures and also to higher dimensional manifolds. We also extend this result to moduli spaces with more general submanifolds as decorations and specialise in the case of decorations being embedded circles.
$\mathbb{R}^\infty$ with particles and discs that are no longer constrained, i.e. the decorations are decoupled. We show that under certain conditions these spaces cannot be distinguished by homology groups within a range. This generalises work by Bödigheimer–Tillmann for oriented surfaces to different tangential structures and also to higher dimensional manifolds. We also extend this result to moduli spaces with more general submanifolds as decorations and specialise in the case of decorations being embedded circles.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 163 - 198
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
- 2
- Cited by

