Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-24T05:27:05.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential equations in Banach spaces and the extension of Lyapunov's method

Published online by Cambridge University Press:  24 October 2008

V. Lakshmikantham
V. Lakshmikantham
Affiliation:
Mathematics Research Center, United States Army, University of Wisconsin
Get access Rights & Permissions [Opens in a new window]

Extract

The concept of Lyapunov's function is an important tool in studying various problems of ordinary differential equations. In the present paper we shall extend the Lyapunov's method to study some problems of differential equations in Banach spaces. Continuing the theory of one parameter semi-groups of linear and bounded operators founded by Hille and Yoshida, Kato(4) presented some uniqueness and existence theorems for the solutions of linear differential equations of the type

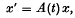
where A(t) is a given function whose values are linear operators in Banach space. Krasnoselskii, Krein and Soboleveskii (5,6) also considered such equations including non-linear differential equations of the type

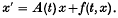
Mlak (9) obtained some results concerning the limitations of solutions of the latter equation.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 2 , April 1963 , pp. 373 - 381
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Antosiewicz, H. A., An inequality for approximate solutions of ordinary differential equations. Math. Z. 8 (1962), 44–52.CrossRefGoogle Scholar
(2)Conti, R., Sulla prolungabilita della soluzioni di un sistema di equazioni differenziali ordinarie. Boll. Un. Mat. Ital. 11 (1956), 510–514.Google Scholar
(3)Coddington, E. A., and Levinson, N., Theory of ordinary differential equations (New York, 1955).Google Scholar
(4)Kato, T., On linear differential equations in Banach spaces. Comm. Pure Appl. Math. 9 (1956), 479–486.CrossRefGoogle Scholar
(5)Krasnoselskii, M. A., Krein, S. G., and Soboleveskii, P. E., On differential equations with unbounded operators in Banach spaces. Dokl. Akad. Nauk. SSSR, 111 (1956), 19–22.Google Scholar
(6)Krasnoselskii, M. A., Krein, S. G., and Soboleveskii, P. E., On differential equations with unbounded operators in a Hilbert space. Dokl. Akad. Nauk. SSSR, 112 (1957), 990–993.Google Scholar
(7)Lakshmikanth, V., On the boundedness of solutions of non-linear differential equations. Proc. American Math. Soc. 8 (1957), 1044–1048.Google Scholar
(8)Lakshmikantham, V., Differential systems and extension of Lyapunov method. Michigan Math. J. 9 (1962), 311–320.CrossRefGoogle Scholar
(9)Mlak, W., Limitations and dependence on parameter of solutions of non-stationary differential operator equations. Ann. Polon. Math. 6 (1959), 305–322.CrossRefGoogle Scholar
(10)Yoshizawa, T., Lyapunov's function and boundedness of solutions. Funkcial. Ekvac. 2 (1959), 95–142.Google Scholar
(11)Wintner, A., The infinities in the non-local existence problem of ordinary differential equations. American J. Math. 68 (1946), 173–178.CrossRefGoogle Scholar