Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wilson, John S.
1985.
On products of soluble groups of finite rank.
Commentarii Mathematici Helvetici,
Vol. 60,
Issue. 1,
p.
337.
Kurdachenko, L. A.
and
Tushev, A. V.
1986.
Some classes of groups with weak minimal condition for normal subgroups.
Ukrainian Mathematical Journal,
Vol. 37,
Issue. 4,
p.
364.
Kurdachenko, L. A.
Kuzennyi, N. F.
and
Semko, N. N.
1992.
Groups with a dense system of infinite almost normal subgroups.
Ukrainian Mathematical Journal,
Vol. 43,
Issue. 7-8,
p.
904.
Gudivok, P. M.
Vashchuk, F. G.
and
Drobotenko, V. S.
1992.
Chernikov p-groups and integral p-adic representations of finite groups.
Ukrainian Mathematical Journal,
Vol. 44,
Issue. 6,
p.
668.
Haug, Frieder
1994.
On Preservation of Stability for Finite Extensions of Abelian Groups.
Mathematical Logic Quarterly,
Vol. 40,
Issue. 1,
p.
14.
Tomkinson, M. J.
1995.
Schunck classes and projectors in a class of locally finite groups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 38,
Issue. 3,
p.
511.
Heineken, Hermann
and
Kurdachenko, Leonid A.
1995.
Groups with subnormality for all subgroups that are not finitely generated.
Annali di Matematica Pura ed Applicata,
Vol. 169,
Issue. 1,
p.
203.
Tushev, Anatolii V.
1996.
Spectra of conjugated ideals in group algebras of abelian groups of finite rank and control theorems.
Glasgow Mathematical Journal,
Vol. 38,
Issue. 3,
p.
309.
Gudivok, P. M.
and
Shapochka, I. V.
1999.
On Chernikovp-groups.
Ukrainian Mathematical Journal,
Vol. 51,
Issue. 3,
p.
329.
Ballester-Bolinches, A.
and
Camp-Mora, S.
1999.
A Gaschütz–Lubeseder Type Theorem in a Class of Locally Finite Groups.
Journal of Algebra,
Vol. 221,
Issue. 2,
p.
562.
Гудивок, П. М.
and
Шапочка, И. В.
1999.
О черниковскихp-группах.
Ukrainian Mathematical Journal,
Vol. 51,
Issue. 3,
p.
291.
Kurdachenko, L. A.
and
Subbotin, I. Ya.
2001.
ON SOME INFINITE DIMENSIONAL LINEAR GROUPS.
Communications in Algebra,
Vol. 29,
Issue. 2,
p.
519.
Cutolo, Giovanni
and
Nicotera, Chiara
2002.
A note on endomorphisms of hypercentral groups.
Journal of Algebra,
Vol. 255,
Issue. 1,
p.
164.
Russo, Francesco
2007.
Anti-CC-Groups and Anti-PC-Groups.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2007,
Issue. ,
p.
1.
Kurdachenko, Leonid A
Muñoz-Escolano, José M
and
Otal, Javier
2008.
Antifinitary linear groups.
Forum Mathematicum,
Vol. 20,
Issue. 1,
Kurdachenko, Leonid A.
Subbotin, Igor Ya.
and
Chupordya, Vasiliy A.
2015.
On Modules with Few Minimax Cocentralizers.
Communications in Algebra,
Vol. 43,
Issue. 2,
p.
871.
Lv, Heng
Chen, Guiyun
and
Zhou, Wei
2017.
The power structure of locally nilpotent $$\varvec{p}$$ p -groups.
Archiv der Mathematik,
Vol. 108,
Issue. 2,
p.
123.
Arikan, Ahmet
Cutolo, Giovanni
and
Robinson, Derek J.S.
2018.
On groups that are dominated by countably many proper subgroups.
Journal of Algebra,
Vol. 509,
Issue. ,
p.
445.
De Falco, M.
de Giovanni, F.
Kurdachenko, L.A.
and
Musella, C.
2018.
The metanorm and its influence on the group structure.
Journal of Algebra,
Vol. 506,
Issue. ,
p.
76.
de Giovanni, F.
Trombetti, M.
and
Wehrfritz, B. A. F.
2021.
Linear groups whose proper subgroups are close to being nilpotent.
Communications in Algebra,
Vol. 49,
Issue. 7,
p.
3020.
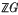 . Suppose that A+ is, furthermore, a divisible p-group, where p is a prime. Since the endomorphism ring
. Suppose that A+ is, furthermore, a divisible p-group, where p is a prime. Since the endomorphism ring 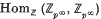 of a quasi-cyclic p-group is isomorphic to the ring
of a quasi-cyclic p-group is isomorphic to the ring 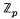 of p-adic integers, we find that
of p-adic integers, we find that 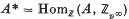 is a free
is a free 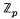 -module of finite rank. We can make A* into a right
-module of finite rank. We can make A* into a right 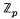 G-module in the usual way, and since A* is actually just the Pontrjagin dual of A, Pontrjagin duality shows that A → A* gives rise to a contravariant equivalence between the categories of divisible Černikov p-torsion modules over
G-module in the usual way, and since A* is actually just the Pontrjagin dual of A, Pontrjagin duality shows that A → A* gives rise to a contravariant equivalence between the categories of divisible Černikov p-torsion modules over 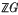 and
and 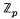 G-modules which are
G-modules which are 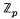 -free of finite rank. Since the latter category is to some extent familiar, at least when G is finite – for its objects determine representations of G over the field
-free of finite rank. Since the latter category is to some extent familiar, at least when G is finite – for its objects determine representations of G over the field 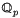 of p-adic numbers, a field of characteristic zero – we may hope to exploit this correspondence systematically to study divisible Černikov p-modules. This is our main theme.
of p-adic numbers, a field of characteristic zero – we may hope to exploit this correspondence systematically to study divisible Černikov p-modules. This is our main theme.

