Published online by Cambridge University Press: 24 October 2008
In this paper, a study is made of the properties of the motion due to a general localized disturbance in an infinite fluid initially at rest. Two invariants of the motion are found, which are identified with the net linear momentum, or effective dipole strength, and the net angular momentum imparted to the fluid, and an equation is derived expressing the rate of change of the effective quadrupole strength of the motion. Solutions are obtained for the final period of decay of such a motion, and it is shown that, when the net linear momentum of the fluid is non-zero, the motion corresponds to a type of viscous vortex ring. The length scale increases with time t as [ν(t – t0)]½, and the total energy decays as [v(t–t0)]-1, where ν is the kinematic viscosity and t0 is a virtual time origin. If the net momentum is zero, the total energy decays as 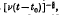 , and expressions are given for the velocity field in this case also.
, and expressions are given for the velocity field in this case also.
It is shown that, if it is attained, the final period of any turbulent motion can be found from the vortex ring type of solution described above. The final period of homogeneous turbulence is clearly one particular example of such a motion. The final period of an axially symmetrical turbulent wake is treated in this way and is shown to consist generally of the superposition of two types of motion: (i) a mean streaming motion whose energy per unit length of the wake decreases as [ν(t – t0)]-1, and (ii) a superimposed fluctuating motion whose energy per unit length decays as [v(t–t0)]-1. Expressions are given for the distribution of mean-square vorticity and the energy spectrum tensor in the wake.