Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T14:32:36.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Hölder differentiability of self-conformal devil's staircases

Published online by Cambridge University Press:  09 January 2014

SASCHA TROSCHEIT
SASCHA TROSCHEIT*
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews, KY16 9SS, Scotland. e-mail: st76@st-andrews.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider the probability distribution function of a Gibbs measure supported on a self-conformal set given by an iterated function system (devil's staircase) applied to a compact subset of 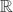${\mathbb R}$. We use thermodynamic multifractal formalism to calculate the Hausdorff dimension of the sets Sα0, Sα∞ and Sα, the set of points at which this function has, respectively, Hölder derivative 0, ∞ or no derivative in the general sense. This extends recent work by Darst, Dekking, Falconer, Kesseböhmer and Stratmann, and Yao, Zhang and Li by considering arbitrary such Gibbs measures given by a potential function independent of the geometric potential.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 2 , March 2014 , pp. 295 - 311
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bowen, R.Equilibrium states and the ergodic theory of Anosov diffeomorphisms, Lecture Notes in Math. vol. 470 (Springer-Verlag, Berlin, revised edition, 2008). With a preface by David Ruelle, Edited by Jean-René Chazottes.Google Scholar
[2]Darst, R.The Hausdorff dimension of the nondifferentiability set of the Cantor function is [ln(2)/ln(3)]2. Proc. Amer. Math. Soc. 119 (1) (1993), 105–108.Google Scholar
[3]Darst, R.Hausdorff dimension of sets of non-differentiability points of Cantor functions. Math. Proc. Camb. Phil. Soc. 117 (1) (1995), 185–191.Google Scholar
[4]Falconer, K.Techniques in Fractal Geometry. (John Wiley & Sons Ltd., Chichester, 1997).Google Scholar
[5]Falconer, K. J.One-sided multifractal analysis and points of non-differentiability of devil's staircases. Math. Proc. Camb. Phil. Soc. 136 (1) (2004), 167–174.Google Scholar
[6]Kesseböhmer, M. and Stratmann, B. O.Hölder-differentiability of Gibbs distribution functions. Math. Proc. Camb. Phil. Soc. 147 (2) (2009), 489–503.Google Scholar
[7]Li, W.Non-differentiability points of Cantor functions. Math. Nachr. 280 (1–2) (2007), 140–151.Google Scholar
[8]Morris, J.The Hausdorff dimension of the nondifferentiability set of a nonsymmetric Cantor function. Rocky Mountain J. Math. 32 (1) (2002), 357–370.Google Scholar
[9]Pesin, Y. and Weiss, H.The multifractal analysis of Gibbs measures: motivation, mathematical foundation, and examples. Chaos 7 (1) (1997), 89–106.Google Scholar
[10]Pesin, Y. B.Dimension theory in dynamical systems. Chicago Lectures in Mathematics. (University of Chicago Press, Chicago, IL, 1997). Contemporary views and applications.Google Scholar
[11]Ruelle, D.Thermodynamic formalism. Cambridge Mathematical Library (Cambridge University Press, Cambridge, second edition, 2004). The mathematical structures of equilibrium statistical mechanics.Google Scholar
[12]Yao, Y., Zhang, Y. and Li, W.Dimensions of non-differentiability points of Cantor functions. Studia Math. 195 (2) (2009), 113–125.CrossRefGoogle Scholar