Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T04:16:35.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Incomplete reflexive spaces without Schauder bases

Published online by Cambridge University Press:  24 October 2008

R. J. Knowles  and
T. A. Cook
R. J. Knowles
Affiliation:
University of Connecticut, Waterbury Branch, Waterbury, Connecticut
T. A. Cook
Affiliation:
University of Massachusetts, Department of Mathematics, Amherst, Massachusetts
Get access Rights & Permissions [Opens in a new window]

Extract

In 1968, Amemiya and Kōmura ((1), p. 275) gave an example of a separable and incomplete Montel space. Their example depended upon constructing a subspace of ω, the countable product of real lines, which had several properties and in particular had codimension 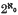in ω. There is an error on page 276, line 5 of the proof of the Hilfssatz concerning this construction. The constructed subspace has codimension one. A more delicate construction is needed here; in fact, an example given by Webb ((7), p. 360) is sufficient to make this correction.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 1 , July 1973 , pp. 83 - 86
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Amemiya, I. and Kömura, Y.Über nicht-völlständige Montel Raume. Math. Ann. 177 (1968), 273–277. MR 38 no. 508.CrossRefGoogle Scholar
(2)Garling, D. J. H. and Kalton, N. J.Proceedings of the international colloquium on nuclear spaces and ideals in operator algebras, Part III. Studia Math. 38 (1970), 474.Google Scholar
(3)Kalton, N. J.A barrelled space without a basis. Proc. Amer. Math. Soc. 26 (1970), 465–466.CrossRefGoogle Scholar
(4)Knowles, R. J. Schauder bases, bounded finiteness, and sumrnability bases in locally convex spaces. Dissertation at U. of Massachusetts, Amherst, 1972.Google Scholar
(5)Robertson, J. M. and Wiser, H. C.A note on polar topologies. Canad. Math. Bull. 11 (1968), 607–609. MR 39 no. 750.CrossRefGoogle Scholar
(6)Schaefer, H. H.Topological vector spaces. (New York, Macmillan, 1966).Google Scholar
(7)Webb, J. H.Sequential convergence in locally convex spaces. Proc. Cambridge Philos. Soc. 64 (1968), 341–364. MR 36 no. 5652.CrossRefGoogle Scholar