Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T21:35:59.121Z Has data issue: false hasContentIssue false
  • English
  • Français

A monoidal algebraic model for rational SO(2)-spectra

Published online by Cambridge University Press:  11 April 2016

DAVID BARNES
DAVID BARNES*
Affiliation:
Pure Mathematics Research Centre, Queen's University Belfast, Belfast, BT7 1NN. e-mail: d.barnes@qub.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The category of rational SO(2)–equivariant spectra admits an algebraic model. That is, there is an abelian category 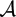${\mathcal A}$(SO(2)) whose derived category is equivalent to the homotopy category of rational SO(2)–equivariant spectra. An important question is: does this algebraic model capture the smash product of spectra?

The category 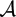${\mathcal A}$(SO(2)) is known as Greenlees' standard model, it is an abelian category that has no projective objects and is constructed from modules over a non–Noetherian ring. As a consequence, the standard techniques for constructing a monoidal model structure cannot be applied. In this paper a monoidal model structure on 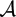${\mathcal A}$(SO(2)) is constructed and the derived tensor product on the homotopy category is shown to be compatible with the smash product of spectra. The method used is related to techniques developed by the author in earlier joint work with Roitzheim. That work constructed a monoidal model structure on Franke's exotic model for the K(p)–local stable homotopy category.

A monoidal Quillen equivalence to a simpler monoidal model category R•-mod that has explicit generating sets is also given. Having monoidal model structures on 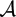${\mathcal A}$(SO(2)) and R•-mod removes a serious obstruction to constructing a series of monoidal Quillen equivalences between the algebraic model and rational SO(2)–equivariant spectra.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 1 , July 2016 , pp. 167 - 192
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barnes, D.Classifying rational G-spectra for finite G. Homology, Homotopy Appl. 11 (1) (2009), 141–170.Google Scholar
[2]Barnes, D. and Roitzheim, C.Monoidality of Franke's exotic model. Adv. Math. 228 (6) (2011), 3223–3248.Google Scholar
[3]Barnes, D. and Roitzheim, C.Stable left and right Bousfield localisations. Glasgow Mathematical Journal FirstView. 2 (2013), 1–30.Google Scholar
[4]Barwick, C.On left and right model categories and left and right Bousfield localisations. Homology, Homotopy Appl. 12 (2) (2010), 245–320.Google Scholar
[5]Beke, T.Sheafifiable homotopy model categories. Math. Proc. Camb. Phil. Soc. 129 (3) (2000), 447–475.Google Scholar
[6]Borceux, F.Handbook of categorical algebra. 2, Encycl. Math. Appl. vol. 51 (Cambridge University Press, Cambridge, 1994). Categories and structures.Google Scholar
[7]Bousfield, A. K.A classification of K-local spectra. J. Pure Appl. Algebra 66 (2) (1990), 121–163.Google Scholar
[8]Greenlees, J. P. C.Rational O(2)-equivariant cohomology theories. In Stable and Unstable homotopy (Toronto, ON, 1996), volume 19 of Fields Inst. Commun. (Amer. Math. Soc., Providence, RI, 1998), pages 103–110.Google Scholar
[9]Greenlees, J. P. C.Rational S 1-equivariant stable homotopy theory. Mem. Amer. Math. Soc. 138 (661) (1999), xii+289.Google Scholar
[10]Greenlees, J. P. C.Rational torus-equivariant stable homotopy. I. Calculating groups of stable maps. J. Pure Appl. Algebra 212 (1) (2008), 72–98.Google Scholar
[11]Greenlees, J. P. C. and Shipley, B. An algebraic model for rational torus-equivariant spectra. arXiv: 1101:2511, (2016).Google Scholar
[12]Greenlees, J. P. C. and Shipley, B.Homotopy theory of modules over diagrams of rings. Proc. Amer. Math. Soc. Ser. B 1 (2014), 89–104.Google Scholar
[13]Greenlees, J.P.C.Rational torus-equivariant stable homotopy II: Algebra of the standard model. J. Pure Appl. Algebra 216 (10) (2012), 2141–2158.Google Scholar
[14]Hirschhorn, P. S.Model categories and their localizations. Math. Surv. Monogr. vol. 99 (American Mathematical Society, Providence, RI, 2003).Google Scholar
[15]Hovey, M.Model categories, Math. Surv. Monogr. vol. 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
[16]Hovey, M.Homotopy theory of comodules over a Hopf algebroid. In Homotopy theory: relations with algebraic geometry, group cohomology, and algebraic K-theory. Contemp. Math. vol. 346 (Amer. Math. Soc., Providence, RI, 2004), pages 261–304.Google Scholar
[17]Lewis, L. G. Jr., May, J. P., Steinberger, M. and McClure, J. E.Equivariant stable homotopy theory. Lecture Notes in Math. vol. 1213 (Springer-Verlag, Berlin, 1986). With contributions by J. E. McClure.Google Scholar
[18]Roitzheim, C.On the algebraic classification of K-local spectra. Homology, Homotopy Appl. 10 (1) (2008), 389–412.Google Scholar
[19]Shipley, B.H $\mathbb{Z}$-algebra spectra are differential graded algebras. Amer. J. Math. 129 (2) (2007), 351–379.Google Scholar