Non-homogeneous binary cubic forms
Published online by Cambridge University Press: 24 October 2008
Extract
1. Let f(x1, x2, …, xn) be a homogeneous form with real coefficients in n variables x1, x2, …, xn. Let a1, a2, …, an be n real numbers. Define mf(a1, …, an) to be the lower bound of | f(x1 + a1, …, xn + an) | for integers x1, …, xn. Let mf be the upper bound of mf(a1, …, an) for all choices of a1, …, an. For many forms f it is known that there exist estimates for mf in terms of the invariants alone of f. On the other hand, it follows from a theorem of Macbeath* that no such estimates exist if the region

has a finite volume. However, for such forms there may be simple estimates for mf dependent on the coefficients of f; for example, Chalk has conjectured that:
If f(x,y) is reduced binary cubic form with negative discriminant, then for any real a, b there exist integers x, y such that
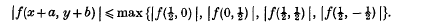
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 3 , July 1951 , pp. 457 - 460
- Copyright
- Copyright © Cambridge Philosophical Society 1951
References
* See p. 627.
† In the sense of Davenport, , J. London Math. Soc. 20 (1945), 139–47.CrossRefGoogle Scholar
‡ Cambridge Ph.D., 1950.
§ See Davenport, , J. London Math. Soc. 20 (1945), 14–22.CrossRefGoogle Scholar
- 6
- Cited by

