Notes on a theorem of Cochran
Published online by Cambridge University Press: 24 October 2008
Extract
1. General remarks. The theorem that has come to be known as Cochran's theorem in works on mathematical statistics was published in these Proceedings in 1934(1). If x1, …, xn are independently distributed standard normal deviates, and q1, …, qk are k real quadratic forms in the xi with ranks n1, …, nk respectively, and such that 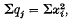 then Cochran's Theorem II states that a necessary and sufficient condition that q1 …, qk are independently distributed in χ2 forms with n1, …, nk degrees of freedom is that Σnj = n. The necessity of the condition is obvious. Cochxan proves its sufficiency by expressing each qj as a sum,
then Cochran's Theorem II states that a necessary and sufficient condition that q1 …, qk are independently distributed in χ2 forms with n1, …, nk degrees of freedom is that Σnj = n. The necessity of the condition is obvious. Cochxan proves its sufficiency by expressing each qj as a sum, 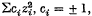 involving nj squares of real linear forms in the xi; it follows easily that the coefficients ci are in fact + 1, and that the transformation is orthogonal. The theorem then follows immediately from the properties of orthogonal transformations in relation to independent normal deviates.
involving nj squares of real linear forms in the xi; it follows easily that the coefficients ci are in fact + 1, and that the transformation is orthogonal. The theorem then follows immediately from the properties of orthogonal transformations in relation to independent normal deviates.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 3 , July 1952 , pp. 443 - 446
- Copyright
- Copyright © Cambridge Philosophical Society 1952
References
REFERENCES
- 14
- Cited by

