Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Smith, R. R.
1981.
The numerical range in the second dual of a Banach algebra.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 89,
Issue. 2,
p.
301.
Flinn, P. H.
and
Smith, R. R.
1984.
𝑀-structure in the Banach algebra of operators on 𝐶₀(Ω).
Transactions of the American Mathematical Society,
Vol. 281,
Issue. 1,
p.
233.
Iochum, B.
and
Loupias, G.
1989.
Arens regularity and local reflexivity principle for Banach algebras.
Mathematische Annalen,
Vol. 284,
Issue. 1,
p.
23.
Li, Chi-Kwong
Rodman, Leiba
and
Spitkovsky, Ilya M.
2003.
On numerical ranges and roots.
Journal of Mathematical Analysis and Applications,
Vol. 282,
Issue. 1,
p.
329.
Blecher, David P.
and
Read, Charles John
2011.
Operator algebras with contractive approximate identities.
Journal of Functional Analysis,
Vol. 261,
Issue. 1,
p.
188.

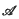 the real subspace
the real subspace 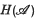 of hermitian elements deserves special attention. This forms the natural generalization of the set of self-adjoint elements in a C*-algebra and exhibits many of the same properties. Two equivalent definitions may be given:
of hermitian elements deserves special attention. This forms the natural generalization of the set of self-adjoint elements in a C*-algebra and exhibits many of the same properties. Two equivalent definitions may be given: 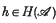 if
if 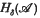 , where
, where 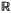 . In this paper some related subsets
. In this paper some related subsets 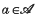 is said to be a member of
is said to be a member of 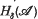 if the condition
if the condition