Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T03:30:01.548Z Has data issue: false hasContentIssue false
  • English
  • Français

On block Behrend sequences

Published online by Cambridge University Press:  24 October 2008

G. Tenenbaum
G. Tenenbaum
Affiliation:
Institut Élie Cartan, Université Henri Poincaré-Nancy 1, BP 239, 54506 Vandœuvre Cedex, France
Get access Rights & Permissions [Opens in a new window]

Extract

Let A be a strictly increasing sequence of integers exceeding 1 and let

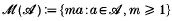
denote its set of multiples. We say that A is a Behrend sequence if M(A) has asymptotic density 1. The theory of sets of multiples was first developed in the late thirties, under the influence of Erdős, Besicovitch, and others. An account of the classical notions is presented in the book of Halberstam and Roth (1966), and recent progress in the area may be found in Hall and Tenenbaum [7], Erdős and Tenenbaum [4], Ruzsa and Tenenbaum [9]. As underlined by Erdős in [3], one of the central problems in the field is that of finding general criteria to decide whether a given sequence A is Behrend.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 2 , August 1996 , pp. 355 - 367
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Davenport, H. and Erdős, P.. On sequences of positive integers. Acta Arith. 2 (1937), 147–151.CrossRefGoogle Scholar
[2]Davenport, H. and Erdős, P.. On sequences of positive integers. J. Indian Math. Soc. 15 (1951), 19–24.Google Scholar
[3]Erdős., P.Some unconventional problems in number theory. Astérisque 61 (1979), 73–92.Google Scholar
[4]Erdős., P., Hall, R. R. and Tenenbaum, G.. On the densities of sets of multiples. J. reine angew. Math. 454 (1994), 119–141.Google Scholar
[5]Halberstam, H. and Richert, H.-E.. Sieve methods (Academic Press, 1974).Google Scholar
[6]Hall, R. R. and Tenenbaum, G.. Divisors (Cambridge University Press, 1988).CrossRefGoogle Scholar
[7]Hall, R. R. and Tenenbaum, G.. On Behrend sequences. Math. Proc. Camb. Phil. Soc. 112 (1992), 467–482.CrossRefGoogle Scholar
[8]Maier, H. and Tenenbaum, G.. On the set of divisors of an integer. Invent. Math. 76 (1984), 121–128.CrossRefGoogle Scholar
[9]Ruzsa, I. and Tenenbaum, G.. A note on Behrend sequences. Acta Math. Hung. (to appear).Google Scholar
[10]Shiu, P.. A Brun–Titchmarsh theorem for multiplicative functions. J. reine angew. Math. 313 (1980), 161–170.Google Scholar
[11]Tenenbaum, G.. Sur la probabilité qu'un entier possède un diviseur dans un intervalle donné. Compositio Math. 51 (1984), 243–263.Google Scholar
[12]Tenenbaum, G.. Uniform distribution on divisors and Behrend sequences. Enseign. Math. to appear.Google Scholar