No CrossRef data available.
On 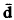 -convergence of Markov chains
-convergence of Markov chains
Published online by Cambridge University Press: 24 October 2008
Extract
Let I be a countable set, with discrete topology, and let X = (Xn), Y = (Yn) be stationary stochastic processes taking values in I. To a probabilist, the natural topology on processes (strictly speaking, on distributions of processes) is weak convergence:
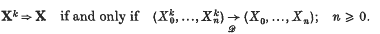
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 2 , September 1981 , pp. 331 - 333
- Copyright
- Copyright © Cambridge Philosophical Society 1981
References
REFERENCES
(1)Ellis, M. H.Distances between two-state Markov processes attainable by Markov joinings. Trans. Amer. Math. Soc. 241 (1978), 129–153.CrossRefGoogle Scholar
(2)Ellis, M. H.On Kamae's conjecture concerning the d-distance between two-state Markov processes. Ann. Probability 8 (1980), 372–376.CrossRefGoogle Scholar
(3)Ellis, M. H.Conditions for attaining d by a Markovian joining. Ann. Probability 8 (1980), 431–440.CrossRefGoogle Scholar
(4)Ornstein, D. S.An application of ergodic theory to probability theory. Ann. Probability 1 (1973), 43–65.CrossRefGoogle Scholar

