On elements of order four in certain free central extensions of groups
Published online by Cambridge University Press: 24 October 2008
Extract
Let F be a non-cyclic free group, R a normal subgroup of F and G = F/R, i.e.

where π is the natural projection of F onto G, is a free presentation of G. Let R′ denote the commutator subgroup of R. The quotient F/[R′,F] is a free central extension
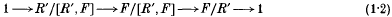
of the group F/R′, the latter being a free abelianized extension of G. While F/R′ is torsion-free (see, e.g. [2], p. 23), elements of finite order may occur in R′/[R′,F], the kernel of the free central extension (l·2). Since C. K. Gupta [1] discovered elements of order 2 in the free centre-by-metabelian group F/[F″,F] (i.e. (1·2) in the case R = F′), torsion in F/[R′,F] has been studied by a number of authors (see, e.g. [4–13]). Clearly the elements of finite order in F/[R′,F] form a subgroup T of the abelian group R′/[R′,F]. It will be convenient to write T additively. By a result of Kuz'min [5], any element of T has order 2 or 4. Moreover, it was pointed out in [5] that elements of order 4 may really occur. On the other hand, it has been shown in [11] that, if G has no 2-torsion, then T is an elementary abelian 2-group isomorphic to H4(G, ℤ2). So if T contains an element of order 4, then G must have 2-torsion. We also mention a result of Zerck [13], who proved that 2T is an invariant of G, i.e. it does not depend on the particular choice of the free presentation (1·1).
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 106 , Issue 1 , July 1989 , pp. 13 - 28
- Copyright
- Copyright © Cambridge Philosophical Society 1989
References
REFERENCES
- 7
- Cited by

