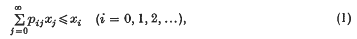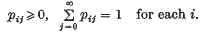Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mauldon, J. G.
1957.
On non-dissipative Markov chains.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 53,
Issue. 4,
p.
825.
Kendall, David G.
and
Reuter, G. E. H.
1957.
The calculation of the ergodic projection for Markov chains and processes with a countable infinity of states.
Acta Mathematica,
Vol. 97,
Issue. 0,
p.
103.
Nash-Williams, C. St J. A.
1959.
Random walk and electric currents in networks.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 55,
Issue. 2,
p.
181.
Bishir, J.
1963.
A Lower Bound for the Critical Probability in the One-Quadrant Oriented-Atom Percolation Process.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 25,
Issue. 2,
p.
401.
Iosifescu, M.
and
Tăutu, P.
1973.
Stochastic processes and applications in biology and medicine I.
Vol. 3,
Issue. ,
p.
11.
Tweedie, Richard L.
1975.
Sufficient conditions for regularity, recurrence and ergodicity of Markov processes.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 78,
Issue. 1,
p.
125.
Samuel-Cahn, Ester
and
Zamir, Shmuel
1977.
Algebraic characterization of infinite Markov chains where movement to the right is limited to one step.
Journal of Applied Probability,
Vol. 14,
Issue. 04,
p.
740.
Samuel-Cahn, Ester
and
Zamir, Shmuel
1977.
Algebraic characterization of infinite Markov chains where movement to the right is limited to one step.
Journal of Applied Probability,
Vol. 14,
Issue. 4,
p.
740.
McGuinness, Sean
1991.
Recurrent networks and a theorem of Nash-Williams.
Journal of Theoretical Probability,
Vol. 4,
Issue. 1,
p.
87.
Kumar, P.R.
and
Meyn, S.P.
1996.
Duality and linear programs for stability and performance analysis of queuing networks and scheduling policies.
IEEE Transactions on Automatic Control,
Vol. 41,
Issue. 1,
p.
4.
Locker, V.F.
and
Wang, P.P.
1997.
The computation of steady-state distribution of parallel systems with two servers.
p.
256.
Kumar, P. R.
2003.
IUTAM Symposium on Nonlinear Stochastic Dynamics.
Vol. 110,
Issue. ,
p.
205.
Anandam, Victor
2013.
Some potential-theoretic techniques in non-reversible Markov chains.
Rendiconti del Circolo Matematico di Palermo,
Vol. 62,
Issue. 2,
p.
273.
McIver, Annabelle
Morgan, Carroll
Kaminski, Benjamin Lucien
and
Katoen, Joost-Pieter
2018.
A new proof rule for almost-sure termination.
Proceedings of the ACM on Programming Languages,
Vol. 2,
Issue. POPL,
p.
1.