Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T11:24:44.519Z Has data issue: false hasContentIssue false
  • English
  • Français

On rational primes p congruent to 1 (mod 3 or 5)

Published online by Cambridge University Press:  24 October 2008

A. R. Rajwade
A. R. Rajwade
Affiliation:
Trinity College, Cambridge†
Get access Rights & Permissions [Opens in a new window]

Extract

Let p ≡ 1 (mod 3) or ≡ 1 (mod 5) be a rational prime and g a primitive root mod p. The non-zero residues g, g2,…,gp−1 (mod p) can then be divided into 3 or 5 classes 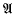, , 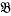, 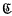or 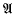, , 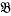, , 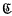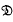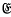respectively, by letting gν ∈ 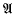, , 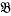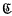(respectively 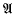, , 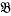, , 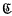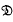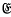) according as ν ≡ 0, 1, 2, (mod 3) (respectively 0, 1, 2, 3, 4 (mod 5)). Problems regarding the distribution of 1, 2, …, p − 1 amongst the 3 (respectively 5) classes are many. In this paper we consider the following problem in some detail (we shall state it here for the case p ≡ 1 (mod 3)). Let α, β, γ be typical members of 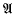, , 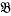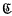respectively. Let the number of solutions of the congruences

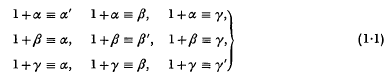
be

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 1 , July 1969 , pp. 61 - 70
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Gauss, C. F.Disquistiones arithmeticae, section 358.Google Scholar
(2)Mathews, G. B.Theory of numbers (Chelsea), Chapter on Cyclotomy.Google Scholar
(3)Rajwade, A. R. Arithmetic on curves with complex multiplication by the Eisenstein integers, section 2. Proc. Cambridge Philos. Soc. (to appear).Google Scholar
(4)Smith, H. J. S.Report on the theory of numbers (Chelsea).Google Scholar
(5)Whiteman, A. L.Cyclotomy and Jacobsthal sums. Amer. J. Math. 74 (1952), 89–99.CrossRefGoogle Scholar