1. In Dirac's classical theory of radiating electrons, the relativistic equations of motion of a point-electron in an electromagnetic field are

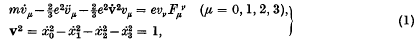
where (x0, x1, x2, x3) denote the electron's coordinates in flat space-time, dots denote differentiation with respect to the proper time 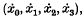, and the external electromagnetic field is described by the usual field quantities Fμν. The units are chosen so that the velocity of light is unity. These equations, which are derived from the principles of conservation of energy and of momentum, are the same as those obtained by Lorentz, when he used the spherical model of the electron and included radiation damping in an approximate way. But Dirac's method of derivation suggests that this treatment of radiation damping, and therefore the resulting scheme of equations, is exact within the limits of the classical theory.