Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T01:47:19.775Z Has data issue: false hasContentIssue false
  • English
  • Français

On the remainder in the two-dimensional central limit theorem

Published online by Cambridge University Press:  24 October 2008

J. E. A. Dunnage
J. E. A. Dunnage
Affiliation:
Chelsea College of Science and Technology, London, S. W. 3
Get access Rights & Permissions [Opens in a new window]

Extract

Our object here is to refine the theorem proved in (3), and we use the notation of that paper. Let Z1, Z2, …, Zn, where Zr = (Xr, Yr), be independent random variables in two dimensions with zero first-order moments and finite third-order moments; and et the covariance matrix of Zr be

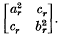
We write

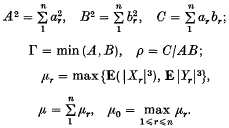
Let 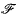(x, y) be the distribution function of the sum 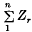and let 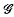(x, y) be the normal distribution function having the same first- and second-order moments as 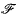(x, y).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 2 , September 1970 , pp. 455 - 458
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bergström, H.On the central limit theorem in the space Rk, k > 1. Skand. Aktuarietidskr. 28 (1945), 106–127.Google Scholar
(2)Bergström, H.On the central limit theorem in the case of not equally distributed random variables. Skand. Aktuarietidskr. 32 (1949), 37–62.Google Scholar
(3)Dunnage, J. E. A.The accuracy of the two-dimensional central limit theorem when degenerate distributions may be present. J. London Math. Soc. (2) 1 (1969), 561–564.CrossRefGoogle Scholar
(4)Sadikova, S. M.Two-dimensional analogues of an inequality of Esseen with applications to the central limit theorem. Theor. Probability Appl. 11 (1966), 325–335. (Translated from Teor. Verojatnost. i. Primenen. 11 (1966), 369–380.)CrossRefGoogle Scholar