No CrossRef data available.
The Problems of Random Flight and Conduction of Heat
Published online by Cambridge University Press: 24 October 2008
Extract
In a paper on random flight Lord Rayleigh proved the following result: A number is formed by adding together n numbers each of which is equally likely to have any value from − a to + a. Then, if f (n, s) ds is the probability that the number so formed lies between s and s + ds, and if n is sufficiently great,
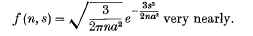
This result may be stated as follows: A point moves discontinuously in a straight line. For a time τ it has a constant velocity. During the next time-interval τ it again has a constant velocity, and so on. Then if each of these velocities is equally likely to have any value from − v to + v, the probability that in the time nτ, the point moves a distance lying between s and s + ds is f (n, s) ds, with vτ written for a.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 2 , May 1924 , pp. 167 - 168
- Copyright
- Copyright © Cambridge Philosophical Society 1924
References
* Phil. Mag. (1919).Google Scholar

