Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T05:16:00.713Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduction modulo pn of p-adic subanalytic sets

Published online by Cambridge University Press:  24 October 2008

Willem Veys
Willem Veys
Affiliation:
K. U. Leuven, Departement Wiskunde, Celestijnenlaan 200-B, B-3001 Leuven, Belgium
Get access Rights & Permissions [Opens in a new window]

Extract

Let ℚp and ℤp respectively denote the p-adic numbers and the p-adic integers for a fixed prime number p. For any subset Y of 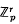and n ∈ ℕ we denote by Nn(Y) the cardinality of the image of Y under the natural map 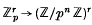. (Thus we have Nn(Y)≤ pnr.)

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 3 , November 1992 , pp. 483 - 486
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bourbaki, N.. Variétés Différentielles et Analytiques. Fascicule de Résultats (Hermann, 1967).Google Scholar
[2]Denef, J.. Multiplicity of the poles of the Poincaré series of a p-adic subanalytic set. Séminaire de Théorie des Nombres de Bordeaux (1987–1988), 43/01–43/08.Google Scholar
[3]Denef, J. and Van Den Dries, L.. p-adic and real subanalytic sets. Ann. of Math. (2) 128 (1988), 79–138.CrossRefGoogle Scholar
[4]Oesterlé, J.. Réduction modulo p n des sous-ensembles analytiques fermés de . Invent. Math. 66 (1982), 325–341.CrossRefGoogle Scholar
[5]Serre, J.-P.. Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54 (1981), 123–201.CrossRefGoogle Scholar