Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T21:00:26.608Z Has data issue: false hasContentIssue false
  • English
  • Français

The remainder in a gap Tauberian theorem for Abel summability

Published online by Cambridge University Press:  24 October 2008

Wolfram Luther
Wolfram Luther
Affiliation:
(Rheinisch-Westfälische Technische Hochschule, Aachen, W. Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Using Pitt's Tauberian classes and a theorem of Pitt (3), Krishnan(2) has recently obtained a gap Tauberian theorem for (Aα) summability. We recall briefly the notation introduced in (2). Let

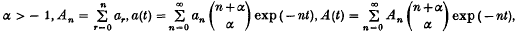
and assume that the series a(t) and A(t) converge for all t > 0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 81 , Issue 1 , January 1977 , pp. 43 - 45
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ganelius, T. H.Tauberian remainder theorems. Lecture Notes in Mathematics 232 (Berlin–Heidelberg–New York Springer 1971).CrossRefGoogle Scholar
(2)Krishnan, V. K.Gap Tauberian theorem for generalized Abel summability. Math. Proc. Cambridge Philos. Soc. 78 (1975), 497–500.CrossRefGoogle Scholar
(3)Pitt, H. R.Tauberian theorems (Tata Institute Monographs No. 2, Oxford University Press 1958).Google Scholar